Bonaventura Cavalieri facts for kids
Quick facts for kids
Bonaventura Cavalieri
|
|
|---|---|
 |
|
| Born |
Bonaventura Francesco Cavalieri
1598 |
| Died | 30 November 1647 (aged 48–49) |
| Nationality | Italian |
| Other names | Bonaventura Cavalerius |
| Alma mater | University of Pisa |
| Known for | Cavalieri's principle Cavalieri's quadrature formula Method of indivisibles Polar coordinate system |
| Scientific career | |
| Fields | Mathematics |
Bonaventura Francesco Cavalieri (Latin: Bonaventura Cavalerius; 1598 – November 30, 1647) was an Italian mathematician and a Jesuate monk. He is famous for his work on optics and motion. He also worked on a method called "indivisibles," which was an early step towards infinitesimal calculus. Cavalieri also helped introduce logarithms to Italy. His Cavalieri's principle in geometry was an important idea that led to integral calculus.
Contents
Cavalieri was born in Milan. When he was fifteen, he joined the Jesuates order of monks. He chose the name Bonaventura. He stayed a monk until he died. In 1615, at age seventeen, he became a full member of the order. Soon after, he went to the Jesuate house in Pisa.
Early Studies and Teaching
By 1616, Cavalieri was studying geometry at the University of Pisa. There, he was taught by Benedetto Castelli. Castelli likely introduced him to the famous scientist Galileo Galilei. In 1617, Cavalieri worked briefly for the Medici family in Florence. But the next year, he went back to Pisa. He started teaching Mathematics in place of Castelli. He tried to get a job as a professor at the University of Bologna, but he was not chosen.
In 1620, he returned to the Jesuate house in Milan, where he had first joined the order. He became a deacon. He studied theology in a monastery in Milan. Later, he became the head of a monastery in Lodi. In 1623, he became the head of another monastery in Parma. But he still wanted to teach mathematics. He applied for jobs in Bologna and then in Rome, but he was turned down each time.
Health and Bologna Appointment
In 1626, Cavalieri started to suffer from gout. This was a painful joint condition that made it hard for him to move for the rest of his life. He was also turned down from a job at the University of Parma. He thought this was because he was a Jesuate monk, and the Jesuits ran Parma at the time.
Finally, in 1629, he was made the Chair of Mathematics at the University of Bologna. Many people believe this happened because Galileo supported him.
Publishing His Work
Cavalieri published most of his important work while he was in Bologna. Some of his writings were actually finished earlier. For example, his book Geometria Indivisibilius was written in 1627. In this book, he explained his "method of indivisibles." But it was not published until 1635. Other mathematicians had different opinions about his work. To answer some of the criticism, he published Six Exercises in Geometry in 1647. While in Bologna, he also published tables of logarithms. He showed people in Italy how to use them.
Galileo had a big impact on Cavalieri. Cavalieri wrote at least 112 letters to Galileo. Galileo once said that "few, if any, since Archimedes, have delved as far and as deep into the science of geometry." Cavalieri also wrote to many other important scientists. These included Marin Mersenne, Evangelista Torricelli, and Vincenzo Viviani. Torricelli especially helped to improve and promote Cavalieri's method of indivisibles.
Towards the end of his life, Cavalieri's health got much worse. Arthritis made it hard for him to write. So, he often told his letters to Stefano degli Angeli, another Jesuate monk and his student, who wrote them down. Angeli later continued to develop Cavalieri's methods.
Cavalieri died in 1647, probably from gout.
Science and Mathematics Work
From 1632 to 1646, Cavalieri published eleven books. These books covered topics like astronomy, optics, motion, and geometry.
Work in Optics
Cavalieri's first book was called Lo Specchio Ustorio, overo, Trattato delle settioni coniche. This means The Burning Mirror, or a Treatise on Conic Sections. It was first published in 1632. The book tried to answer how Archimedes might have used mirrors to burn the Roman fleet. This was a question people still debated.
The book did more than just answer this question. It also looked at conic sections, how light reflects, and the properties of parabolas. In this book, Cavalieri developed ideas about mirrors shaped like parabolas, hyperbolas, and ellipses. He also looked at different ways to combine these mirrors. He showed that if light travels at a certain speed, these mirrors could create clearer images. This was just a theory at the time. People could not build such perfect mirrors with the technology they had. But his ideas could have led to better telescopes than those existing then.
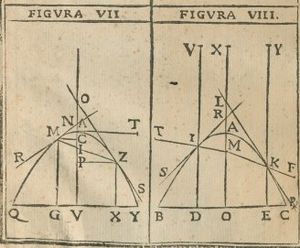
Cavalieri also showed some important properties of curves. For example, he proved that if a light ray hits a parabolic mirror parallel to its axis, it will reflect through a special point called the focus. He showed similar things for hyperbolas and ellipses. Another important idea for designing reflecting telescopes was that if you draw a line from a point outside a parabola to its focus, the reflection of this line on the outside of the parabola will be parallel to its axis.
Lo Specchio Ustorio also had a table of reflecting surfaces. This table showed how different mirrors could be used in practice.
Cavalieri's work also included designs for a new type of telescope that used mirrors. This was a reflecting telescope. He first thought of this to explain Archimedes' Mirror. Then he applied the idea to smaller telescopes. He showed three different ways to use reflective mirrors in his telescope designs.
Work in Geometry and the Method of Indivisibles
Inspired by Galileo, Cavalieri created a new way to solve geometry problems. He called it the method of indivisibles. He wrote a book about it called Geometria indivisibilibus continuorum nova quadam ratione promota. This means Geometry, developed by a new method through the indivisibles of the continua. He wrote it in 1627, but it was published in 1635.
In this book, Cavalieri thought about shapes as being made up of many tiny, parallel "indivisibles." For a flat shape, these indivisibles were like an endless number of parallel lines. For a 3D shape, they were like an endless number of parallel planes. He said that "all the lines" of a shape were related to its area. And "all the planes" were related to its volume. Later mathematicians would say these were equal. But Cavalieri said they were only "comparable."
These parallel elements are the basic parts of Cavalieri's method. They are also key ideas in integral calculus. He used his method to calculate the area under a curve. He found that the area under the curve of x-squared from 0 to 1 is 1/3. He later used this idea for other shapes. For example, he showed that the volume of a cone is one-third the volume of a cylinder that perfectly encloses it.
An important result from the method of indivisibles is Cavalieri's principle. This principle says that two objects have the same volume if the areas of their matching cross-sections are always equal. Imagine slicing two objects at the same height. If every slice has the same area, then the total volumes are the same. (This idea was also used earlier by Zu Gengzhi in China to find the volume of a sphere.)
Cavalieri's method of indivisibles was powerful. But it had some limits. First, his proofs were based on intuition. Even though they were later shown to be correct, they were not always strictly proven at the time. Second, his writing was sometimes hard to understand. Many mathematicians built on his method. But his book Geometria indivisibilibus received some strong criticism.
Cavalieri wrote Exercitationes geometricae sex, or Six Geometric Exercises (1647), to answer these criticisms. He argued that his work looked at "all the lines" as something separate from the area. He also said that "all the lines" and "all the planes" dealt with relative infinity, not absolute infinity. This meant they could be compared. These arguments did not convince everyone at the time. However, the Exercitationes still greatly improved the method of indivisibles. By changing his variables, he made his earlier integral result more general. He showed that the integral of x to the power of n from 0 to 1 is 1/(n+1) for n from 3 to 9. This is now known as Cavalieri's quadrature formula.
Work in Astronomy
Towards the end of his life, Cavalieri published two books about astronomy. Even though they used words from astrology, he said in his books that he did not believe in or practice astrology. These books were Nuova pratica astromlogica (1639) and Trattato della ruota planetaria perpetua (1646).
Other Work
He published tables of logarithms. He showed how useful they were in astronomy and geography.
Cavalieri also built a hydraulic pump for a monastery he managed. The Duke of Mantua later got a similar one.
Legacy

Historians say that Cavalieri, along with scientists like Newton, Leibniz, and Pascal, helped to change how mathematics was understood in the 17th and 18th centuries.
The lunar crater Cavalerius on the Moon is named after Cavalieri.
|
See also
 In Spanish: Bonaventura Cavalieri para niños
In Spanish: Bonaventura Cavalieri para niños
- Evangelista Torricelli
- Stefano degli Angeli
- Cavalieri's quadrature formula