Calculus facts for kids

Calculus is a part of mathematics that helps us understand how things change. Imagine you have a rule that tells you how much money you get each day. Calculus can help you figure out how much money you have in total, or if you are getting more or less money than before. It's all about studying how things change over time.

There are two main types of calculus:

• Differential calculus looks at small changes. It helps us understand how fast something is changing at any exact moment.
• Integral calculus puts small pieces together. It helps us find the total amount of something that has changed over time.

Calculus is used in many different areas, like physics, astronomy, biology, engineering, economics, and medicine.

History of Calculus

In the 1670s and 1680s, two brilliant minds, Sir Isaac Newton in England and Gottfried Leibniz in Germany, developed calculus at the same time. They worked separately.

Newton wanted a new way to predict where planets would be in the sky. Knowing about the movement of objects in space was important for things like navigation for ships. Leibniz wanted to measure the space (area) under a curved line.

Years later, Newton and Leibniz argued about who discovered it first. Today, most mathematicians agree that both men deserve equal credit. Some parts of modern calculus, especially its uses in physics, come from Newton. Other parts, like the symbols we use to write it, come from Leibniz.

Before them, thinkers like Galileo said that mathematics was the language of science. But Newton and Leibniz were the first to create a system that could describe how things change over time and even predict future changes.

The word "calculus" comes from a Latin word for a small stone. Ancient Romans used these stones for counting and gambling. The English word "calculate" also comes from this same Latin word.

Differential Calculus

Differential calculus helps us find out how fast one thing changes compared to another. For example, it can tell us the exact speed of a moving object at any moment. It can also find the steepness (slope) of a curve at any point.

Think about a car driving. Its speed is how far it travels in a certain time. If a town is 80 kilometers (50 miles) away and a car gets there in one hour, the average speed is 80 kilometers per hour. But the car doesn't always go that speed. It might go faster on a highway and slower at a traffic light. Before calculus, figuring out the exact speed at a specific moment was very hard. People had to cut the time into smaller and smaller pieces to get closer to the actual speed.

On a curve, the steepness changes. The red and blue lines are tangents. They show the steepness at specific points.

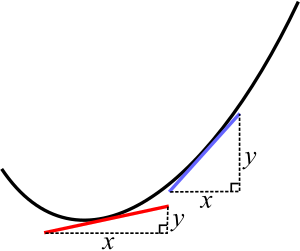
Another similar problem is finding the slope of a curve. A straight line's slope is easy: how much it goes up divided by how much it goes across. But a curve bends, so its slope changes at every point.

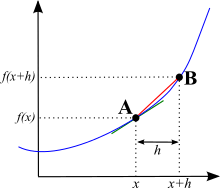
Newton and Leibniz found a way to figure out this exact slope using simple rules. They imagined dividing the curve into an infinite number of tiny pieces. They found that as you look at smaller and smaller parts of the curve, it starts to look like a very short straight line. The slope of this tiny straight line is called a tangent.

This picture shows how we look at two points, x and x + h, on a curve.

This process of finding the exact slope is called differentiation. The result is called the derivative. Mathematicians have developed simple rules to find the derivative of almost any function.

Main Idea of Calculus

The main idea in calculus is called the fundamental theorem of calculus. This big idea says that differential calculus and integral calculus are opposites.

Think of it like this:

• You can use division to "undo" multiplication.
• You can use addition to "undo" subtraction.

In the same way, you can use differential calculus to "undo" an integral calculus process. And you can use integral calculus to "undo" a differential calculus process.

Simply put, the "derivative of the integral of a function is the function itself."

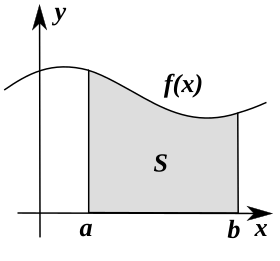
How Integral Calculus Finds Areas

Integration helps us find the area under a curve.

We can guess the area under a curve by adding up many rectangles. More rectangles give a better guess.

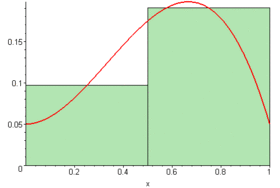
Integral calculus finds the area of shapes by breaking them into many small boxes. Then, it adds up the area of all these boxes. This gives a close guess for the total area.

If the boxes are made narrower and narrower, there will be more and more of them. The total area of all the boxes gets very close to the actual area of the shape. A key idea in calculus is that if we imagine an infinite number of these super-narrow boxes, we can find the exact area of the shape.

Other Uses of Calculus

Calculus is used to describe things that change, especially in nature. It helps us understand:

• How waves move, like sound and light.
• How heat moves, which is useful for architecture to design energy-efficient buildings.
• How tiny things like atoms behave.
• How fast something will fall due to gravity.
• How machines work, which is called mechanics.
• The path of the moon around the earth, or any planet or moon in space.

Images for kids

• 

  Alhazen, an 11th-century Arab mathematician and physicist.

• 

  Maria Gaetana Agnesi, an Italian mathematician.

• 

  The derivative of a curve at a point is the slope of the line that just touches the curve at that point (called a tangent line).

• 

  The spiral shape of the Nautilus shell shows how growth and change can be described by calculus.

See also

In Spanish: Cálculo infinitesimal para niños