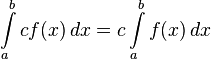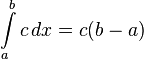Integral facts for kids
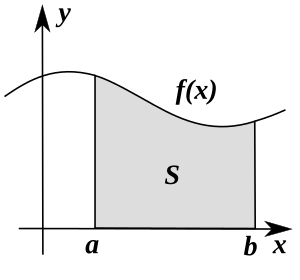
In calculus, an integral helps us find the area under a graph of an equation. Think of it as finding the total space covered by a curve. Integrals are the opposite of derivatives. A derivative tells you how steep a curve is at any point, or how fast something is changing.
The special symbol for integration looks like a tall letter "S": 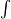 . This symbol was first used by Gottfried Wilhelm Leibniz. He chose it because it looks like a stretched-out "S" from the Latin word summa, which means "sum". This is because integration is like adding up many tiny pieces.
. This symbol was first used by Gottfried Wilhelm Leibniz. He chose it because it looks like a stretched-out "S" from the Latin word summa, which means "sum". This is because integration is like adding up many tiny pieces.
Integrals and derivatives are key parts of a math area called calculus. The way they connect is super important and is called the fundamental theorem of calculus. This theorem shows that an integral can be "undone" by a derivative, just like addition can be undone by subtraction.
Integrals are useful when you need to combine different units in a problem. For example, if you know a rate (like distance per time), and you want to find the total distance, you can use integration. It's like multiplying the rate by time to get just distance. You do this by adding up many tiny "slices" of the rate graph. These slices are super thin, almost zero width, but when you add them all together, they make up a whole. This idea is called a Riemann sum.
Adding these tiny slices helps you find the original equation that the rate came from. Integrals are a powerful way to add up countless small things. It's similar to regular summation, like adding 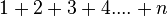 . But with integration, you also add all the tiny decimals and fractions in between.
. But with integration, you also add all the tiny decimals and fractions in between.
Another cool use for integration is finding the volume of a solid object. You can imagine slicing the object into many thin, two-dimensional pieces. Integration adds these slices together, giving them "width" and building up the full three-dimensional volume of the object.
Contents
How to Find Integrals
Antiderivatives: The Reverse Process
The fundamental theorem of calculus tells us that finding an integral is the same as finding an antiderivative. An antiderivative is simply the reverse of a derivative.
For example, if we have the function 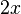 , its antiderivative (or an integral) is
, its antiderivative (or an integral) is 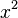 . We say "an" integral, not "the" integral, because there can be many antiderivatives for one function. For instance,
. We say "an" integral, not "the" integral, because there can be many antiderivatives for one function. For instance, 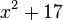 also becomes
also becomes 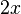 when you take its derivative. This is because the derivative of any constant number (like 17) is always zero.
when you take its derivative. This is because the derivative of any constant number (like 17) is always zero.
Because of this, when you find an antiderivative, you must always add a "plus C" (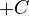 ) at the end. This "C" stands for an unknown constant. This is called an indefinite integral. For example, if you have:
) at the end. This "C" stands for an unknown constant. This is called an indefinite integral. For example, if you have:
Its derivative is:
Notice the "0" from the 15. If we only have 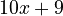 , we can't know what the original constant was. So, the integral is:
, we can't know what the original constant was. So, the integral is:
Integrating Simple Equations
Let's look at a simple equation like 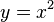 . To integrate it with respect to x, you follow a simple rule:
. To integrate it with respect to x, you follow a simple rule:
- Add 1 to the power that x is raised to.
- Then, divide x by this new power.
So, the general rule for integrating a basic power of x is: 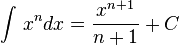
The 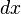 at the end simply shows that we are integrating "with respect to x". This means we are looking at how the function changes as x changes. Remember to always add the constant "C" at the end. This is because when you take the derivative of a constant, it becomes zero. So, when you integrate, you need to account for that possible constant.
at the end simply shows that we are integrating "with respect to x". This means we are looking at how the function changes as x changes. Remember to always add the constant "C" at the end. This is because when you take the derivative of a constant, it becomes zero. So, when you integrate, you need to account for that possible constant.
If an equation has more than one part (or "term"), you just integrate each part separately: 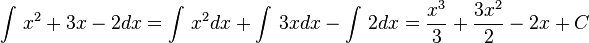
Integrating with e and ln
There are special rules for integrating functions that involve the mathematical constant e (which is about 2.718) and the natural logarithm (ln).
- The integral of
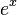 is itself! (Plus the constant of integration, of course):
is itself! (Plus the constant of integration, of course):
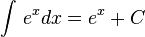
- The natural logarithm, ln, is useful when integrating equations like
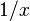 . You can't use the "add one to the power" rule here because that would make the power zero, and you can't divide by zero. Instead, the integral of
. You can't use the "add one to the power" rule here because that would make the power zero, and you can't divide by zero. Instead, the integral of 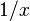 is
is 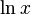 :
:
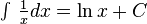
In a more general way, if you have a fraction where the top part is the derivative of the bottom part, its integral is the natural logarithm of the bottom part: 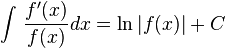 The two vertical bars around
The two vertical bars around 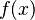 mean "absolute value". This is because you can't take the natural logarithm of a negative number.
mean "absolute value". This is because you can't take the natural logarithm of a negative number.
Properties of Integrals
Adding Functions
When you integrate a sum of functions, it's the same as adding the integrals of each function separately.
This makes sense because integration is like adding up many small parts.
Constants in Integrals
If you have a constant number multiplied by a function inside an integral, you can move the constant outside the integral.
This only works for constants, not for variables.
Also, if you integrate just a constant c by itself, its integral is c times x (when there are no limits). If there are limits from a to b, it's c times the difference between b and a.
Other Useful Rules
- If you have three points a, b, and c in order on the x-axis, the integral from a to b plus the integral from b to c equals the integral from a to c.
: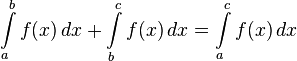
- If the starting and ending points of an integral are the same, the integral is zero. This is because there's no "area" to cover.
: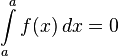
- If you swap the starting and ending points of an integral, the sign of the result changes.
: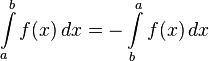
Related Pages
Images for kids
See also
 In Spanish: Integración para niños
In Spanish: Integración para niños


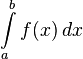
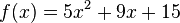
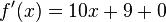
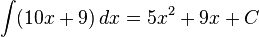
![\int\limits_{a}^{b} [f(x) + g(x)]\, dx = \int\limits_{a}^{b} f(x)\, dx + \int\limits_{a}^{b} g(x)\, dx](/images/math/b/c/8/bc80fcf943487e47ca0f2505517667b1.png)