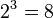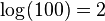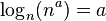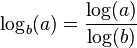Logarithm facts for kids

Logarithms, often called logs, are a special part of mathematics. They help us figure out what power or exponent is needed to get a certain number. Think of them as the opposite of exponentiation, which is when you multiply a number by itself a certain number of times.
For example, if you have 2 multiplied by itself 3 times, you get 8 (which is 23 = 8). A logarithm asks the opposite: "What power do I need to raise 2 to, to get 8?" The answer is 3. We write this as 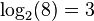 .
.
In this example, 2 is called the base, 8 is the argument, and 3 is the answer (or the exponent).
There are a few common types of logarithms:
- Common logarithms use 10 as their base.
- Binary logarithms use 2 as their base.
- Natural logarithms use a special number called e (which is about 2.71828) as their base.
Logarithms were once very important for multiplying and dividing really big numbers quickly, before calculators were invented!
Contents
- The History of Logarithms
- Logarithms and Exponential Functions: Opposites!
- How Logarithms Differ from Roots
- Real-World Uses of Logarithms
- Common Logarithms: Base 10
- Natural Logarithms: Base e
- Common Bases for Logarithms
- Key Properties of Logarithms
- Logarithm Tables and Slide Rules: Tools of the Past
- Related Topics
- Images for kids
- See also
The History of Logarithms
Logarithms have a long history! People in India were using ideas similar to logarithms as far back as the 2nd century BC.
In more recent times, a German mathematician named Michael Stifel (who lived from about 1487 to 1567) wrote down some important equations in 1544. These equations showed that when you multiply numbers with exponents, you can add their exponents: 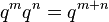 . And when you divide them, you subtract the exponents:
. And when you divide them, you subtract the exponents: 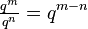 . This was a key step to understanding logarithms.
. This was a key step to understanding logarithms.
Later, John Napier (1550–1617) from Scotland took these ideas further. He wanted to use exponents that weren't just whole numbers. Napier thought of logarithms as a way to compare how numbers change in relation to each other.
At first, a base similar to the number e was used. But another mathematician, Henry Briggs, suggested using 10 as the base. Logarithms with base 10 became very useful, especially in fields like astronomy.
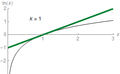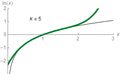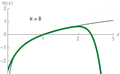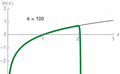
Logarithms and Exponential Functions: Opposites!
Logarithms and exponential functions are like two sides of the same coin. They are inverse operations, meaning they undo each other.
Let's look at an exponential function:
Here, 2 is the base, 3 is the exponent (or power), and 8 is the answer.
Now, let's see its inverse, the logarithmic equation:
In this case, 2 is still the base, 8 is the argument, and 3 is the answer. Notice how the base stays the same, and the exponent and answer swap places!
How Logarithms Differ from Roots
When you add numbers, the opposite is subtraction. When you multiply, the opposite is division. But with exponentiation, there are actually two opposite operations: roots and logarithms.
Why two? Because in exponentiation, the order matters. For example, 2x is usually not the same as x2.
Let's see an example:
- If x + 2 = 3, you subtract to find x = 3 - 2, so x = 1.
- If x multiplied by 2 = 3, you divide to find x =
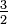 .
. - If x2 = 3, you use a square root to find x =
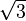 . This finds the base.
. This finds the base. - But if 2x = 3, you can't use a root. Instead, you use a logarithm to find x = log2(3). This finds the exponent.
Real-World Uses of Logarithms
Logarithms are not just for math class; they show up in many places in the real world!
- Nature's Spirals: Many natural patterns follow a Logarithmic spiral shape. You can see this in the shell of a nautilus or how seeds are arranged in a sunflower.
- Chemistry and pH: In chemistry, logarithms are used to measure pH, which tells us how acidic or basic something is. A pH of 7 is neutral, like pure water.
- Earthquake Measurement: The Richter scale measures the strength of earthquakes using a base-10 logarithmic scale. This means an earthquake that is a 6 on the Richter scale is ten times stronger than a 5.
- Star Brightness: In astronomy, the apparent magnitude of stars (how bright they look from Earth) is measured using logarithms. Our eyes actually see brightness in a logarithmic way!
- Music Intervals: Musical intervals (the distance between two notes) are measured using logarithms. For example, a semitone is a logarithmic measure of the frequency ratio between notes.
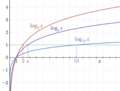
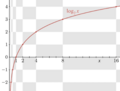
Common Logarithms: Base 10
Logarithms that use 10 as their base are called common logarithms. Often, when you see "log" written without a small number for the base, it means base 10.
For example:
This is true because 10 raised to the power of 2 equals 100:
Natural Logarithms: Base e
Logarithms that use the special number e as their base are called natural logarithms. The number e is approximately 2.71828. It's also known as the Eulerian constant, named after the mathematician Leonhard Euler.
Natural logarithms can be written as 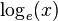 or, more commonly, as
or, more commonly, as 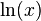 .
.
Common Bases for Logarithms
Here's a quick look at some common bases used for logarithms:
| Base | Abbreviation | What it's used for |
|---|---|---|
| 2 | 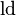 |
Very common in computer science because computers use binary (base-2) numbers. |
| e | 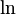 or sometimes or sometimes 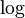 |
The base is the Eulerian constant e. This is the most common logarithm in advanced mathematics. |
| 10 | 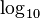 or or 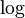 (sometimes (sometimes 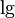 ) ) |
Used in sciences like chemistry and biology. |
| any number, n | 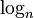 |
This is the general way to write a logarithm with any base. |
Key Properties of Logarithms
Logarithms have some cool properties that make them useful for solving problems.
Properties from the Definition
One property comes straight from what a logarithm is:
This means if the base of the logarithm is the same as the base of the number inside, the answer is just the exponent. For example:
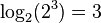
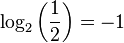 , because
, because  is the same as
is the same as 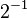 .
.
Another important property lets you change the base of a logarithm:
This means the logarithm of a with base b is the same as the logarithm of a (with any common base, like 10) divided by the logarithm of b (with that same common base). This is super handy for calculators!
Operations Inside Logarithms
Logarithms can turn multiplication into addition and division into subtraction. This is why they were so useful for calculations before computers!
- Multiplication becomes Addition:
: 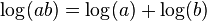 For example, if you want to find
For example, if you want to find 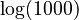 : :
: : 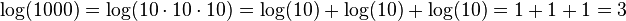
- Division becomes Subtraction:
: 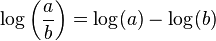
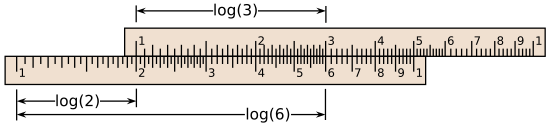
Logarithm Tables and Slide Rules: Tools of the Past
Before electronic calculators, scientists and engineers used logarithms every day. They were essential for calculations in fields like astronomy.
Logarithm tables were books filled with lists of logarithm values. In 1617, Henry Briggs created the first logarithm table. These tables allowed people to look up the logarithm of a number. To multiply two numbers, you would find their logarithms in the table, add those logarithms together, and then find the number that matched the sum in the table. This was much faster than multiplying large numbers by hand!
Another amazing tool was the slide rule. This was a physical device with sliding scales marked with logarithms. By sliding the scales, you could mechanically add or subtract logarithms, which meant you could quickly multiply or divide numbers. Many engineers and scientists used slide rules right up until the 1970s when electronic calculators became common. Slide rules were even faster than using logarithm tables!
Related Topics
Images for kids
-
An explanation of logarithms from the 1797 Encyclopædia Britannica.
See also
 In Spanish: Logaritmo para niños
In Spanish: Logaritmo para niños