Logarithmic spiral facts for kids
Cutaway of a nautilus shell showing the chambers arranged in an approximately logarithmic spiral
|
|
The arms of spiral galaxies often have the shape of a logarithmic spiral, here the Whirlpool Galaxy.
|
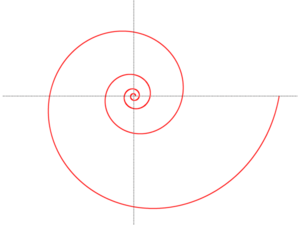
A logarithmic spiral is a special kind of spiral curve that appears often in nature. It's also called an equiangular spiral or growth spiral. The famous mathematician René Descartes first described it. Later, another mathematician named Jakob Bernoulli studied it a lot. He called it Spira mirabilis, which means "the marvelous spiral".
Contents
What is a Logarithmic Spiral?
Imagine a spiral that keeps getting bigger, but its shape always stays the same. That's a logarithmic spiral!
In math, we can describe this curve using a special formula. If you think of a point on the spiral, its distance from the center (called 'r') grows as you go around the spiral (as the angle 'θ' increases). The way it grows is very specific, following a pattern that involves something called an exponential function.
One amazing thing about this spiral is that the angle between a line from the center to any point on the spiral and a line that just touches the spiral at that point (called a tangent) is always the same. This is why it's also called an "equiangular" spiral.
The way the spiral winds, whether it's tight or loose, depends on a number in its formula. If this number is zero, the spiral becomes a circle. If it's very large, the spiral looks almost like a straight line.
Spira Mirabilis: The Marvelous Spiral
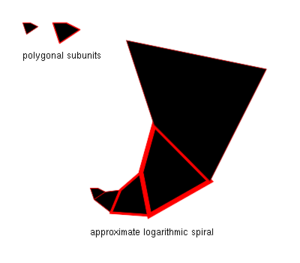
Spira mirabilis is Latin for "miraculous spiral." Jakob Bernoulli gave this name to the logarithmic spiral because he was fascinated by one of its unique properties: as the spiral grows, its size increases, but its shape always stays exactly the same.
Because of this special property, the spira mirabilis shows up in many places in nature. You can see it in the shells of nautilus creatures and even in the patterns of sunflower heads. Jakob Bernoulli was so amazed by this spiral that he wanted it carved on his headstone. However, by mistake, a different kind of spiral, an Archimedean spiral, was put there instead.
Logarithmic Spirals in Nature
You can find shapes very similar to logarithmic spirals in many natural things. Here are some cool examples and why they might appear:
- Hawks hunting: When a hawk flies towards its prey, it often follows a path that looks like a logarithmic spiral. This is because a hawk's sharpest vision is at a certain angle to its direction of flight. To keep its prey in focus, it maintains this constant angle, which naturally leads to a spiral path.
- Insects flying to light: Insects are used to having the sun as their main light source, which is so far away that its rays seem parallel. They usually fly keeping the light source at a constant angle to their flight path. If they do this with a nearby light, like a lamp, they end up flying in a logarithmic spiral towards it.
- Spiral galaxies: The arms of spiral galaxies, like our own Milky Way, often have the shape of a logarithmic spiral. The Milky Way is thought to have four main spiral arms, each roughly a logarithmic spiral.
- Tropical cyclones: The swirling arms of tropical cyclones, like hurricanes, also follow an approximately logarithmic spiral pattern.
- Biological structures: Many living things show this spiral shape. This includes spider webs and the shells of mollusks.
In these biological cases, the spiral forms because of how things grow. Imagine a small shape. If it keeps growing by the same amount in all directions and new parts are added next to the old ones, it naturally forms a logarithmic spiral. The way it expands and the angle at which new parts are added determine how tight the spiral is.
See also
Images for kids
-
A section of the Mandelbrot set following a logarithmic spiral
-
Animation showing the constant angle between an intersecting circle centred at the origin and a logarithmic spiral.
-
A cutaway of a nautilus shell showing its chambers arranged in an approximately logarithmic spiral.
In Spanish: Espiral logarítmica para niños
