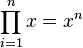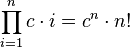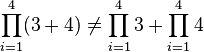Product (mathematics) facts for kids

A product in mathematics is the answer you get when you multiply two or more numbers. For example, if you multiply 4 by 7, the answer is 28. So, 28 is the product of 4 and 7. Another example is 6 multiplied by 4, which gives 24. So, 24 is the product of 6 and 4.

When you multiply two positive numbers, the product is positive. Also, when you multiply two negative numbers, the product is positive. For instance, -6 multiplied by -4 equals 24.

Pi Product Notation

When you need to multiply many numbers together, there's a special shortcut. You can use the capital Greek letter Pi, which looks like this: 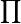. This symbol helps you write long multiplication problems in a short way. It's a bit like the Sigma notation used for adding many numbers.

For example, if you want to multiply numbers like Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a_1, a_2, a_3 , and so on, up to 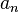, you can write it as Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \prod_{i=1}^n a_i . This simply means Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a_1 \cdot a_2 \cdot \dotsm \cdot a_n . The "i=1" below the Pi means you start with the first number, and the "n" above means you stop at the nth number.

Properties of Products

Here are some interesting properties when using the Pi notation:

• Factorial: If you multiply all whole numbers from 1 up to a certain number n, it's called "n factorial". We write it as .
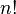  • Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \prod_{i=1}^n i = 1 \cdot 2 \cdot \dots \cdot n = n!
• Powers: If you multiply the same number x by itself n times, it's called x to the power of n ().
  • 
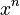• Multiplying a constant: If you multiply a constant number c by each number i in a sequence, you can separate the constant.
  • 

This means that any number with an exponent can be thought of as a product, even if we don't usually write it that way.

Unlike adding, you cannot always separate terms inside a product. For example:

However, if you are multiplying different terms together, you can separate them:

• Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \prod_{i=1}^n a_ib_i=\prod_{i=1}^na_i\prod_{i=1}^nb_i

How Products Relate to Sums

When you multiply numbers that have the same base but different exponents, you can add their exponents together.

• Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \prod_{i=1}^n a^{c_i} = a^{c_1} \cdot a^{c_2} \dotsm a^{c_n}= a^{c_1 + c_2 + \dots + c_n} = a^{(\sum_{i=1}^n c_i)}

This shows a cool connection between multiplication (products) and addition (sums) when dealing with exponents.

Related Pages

• Cartesian product
• Cross product
• Dot product

Images for kids

• 

  The convolution of the square wave with itself gives the triangular function