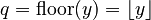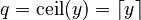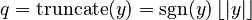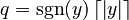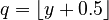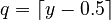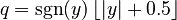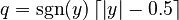Rounding facts for kids
Rounding a number means changing it to a simpler value that's close to the original. It's like estimating! For example, if you have US$23.74, you might round it to US$24. Or, a complicated fraction like 312/937 could be rounded to a simpler 1/3. Even numbers like the square root of 2 (which is about 1.41421356...) can be rounded to 1.41 to make them easier to use.
People often round numbers on purpose. This makes them easier to write, remember, or work with. Rounding can also show how accurate a number is. For instance, if a calculation gives 123,456, but you know it's only accurate to a few hundred units, it's better to say "about 123,500."
However, rounding can cause a small error. This is called a round-off error. It's hard to avoid rounding in many calculations. This is especially true when you divide numbers or work with complex math functions like square roots. These small errors can add up in a series of calculations. Sometimes, they can even make the final answer wrong.
It's very tricky to round some complex math functions perfectly. This is because you don't always know how many extra digits you need to calculate to decide if you should round up or down. This problem is known as "the table-maker's dilemma."
Rounding is similar to how physical measurements are turned into numbers or digital signals. This process is called quantization.
Contents
What are the different ways to round numbers?
Rounding helps us simplify numbers in many situations. Here are some common examples:
- Making an irrational number (a number that can't be written as a simple fraction) into a fraction. For example, π (about 3.14159) can be rounded to 22/7.
- Changing a fraction with a repeating decimal (like 5/3 = 1.6666...) into a shorter decimal. For example, 5/3 can be rounded to 1.6667.
- Turning a rational number (a number that can be written as a fraction) into a fraction with smaller top and bottom numbers. For example, 3122/9417 can be rounded to 1/3.
- Shortening a decimal number by using fewer digits. For example, $2.1784 can be rounded to $2.18.
- Changing a whole number to one with more zeros at the end. For example, 23,217 people can be rounded to 23,200 people.
- Rounding a value to be a multiple of a specific amount. For example, 27.2 seconds might be rounded to 30 seconds (a multiple of 15).
How to round to a specific amount
Often, we round numbers to the nearest whole number. Or, we might round to a multiple of a certain amount. This could be whole tenths of seconds, hundredths of a dollar, or even whole dozens.
To round a number x to a multiple of an amount m, you follow these steps:
- Divide x by m. Let's call this result y.
- Round y to the nearest whole number. Let's call this q.
- Multiply q by m. This gives you the rounded value, z.
For example, imagine you want to round $2.1784 to the nearest cent (which is a multiple of $0.01). First, divide $2.1784 by $0.01. This gives you 217.84. Next, round 217.84 to the nearest whole number, which is 218. Finally, multiply 218 by $0.01. The rounded amount is $2.18.
When you round to a certain number of significant digits, the amount m changes. It depends on how big the number you are rounding is.
Computers often use the binary system (base 2) for rounding. But for people, we usually use the decimal system (base 10).
How to round to a whole number
The simplest way to round is to change any number into a whole number. Here are some common ways to do this:
- Round down (or floor): This means finding the largest whole number that is not bigger than your number.
- Round up (or ceiling): This means finding the smallest whole number that is not smaller than your number.
- Round towards zero (or truncate): This means just dropping the decimal part of the number.
- Round away from zero: If the number is already a whole number, it stays the same. Otherwise, it's the whole number closest to zero that is outside the original number.
- Round to nearest: This means picking the whole number that is closest to your number. (We'll talk about what to do if it's exactly in the middle soon!)
The first four methods are called directed rounding. This is because you always round in a specific direction (towards zero, away from zero, up, or down).
If your number is positive, rounding down is the same as rounding towards zero. Rounding up is the same as rounding away from zero. If your number is negative, it's the opposite. If your number is already a whole number, it doesn't change.
Look at this table to see how these methods work:
| y | round down (towards −∞) |
round up (towards +∞) |
round towards zero |
round away from zero |
round to nearest |
|---|---|---|---|---|---|
| +23.67 | +23 | +24 | +23 | +24 | +24 |
| +23.50 | +23 | +24 | +23 | +24 | +23 or +24 |
| +23.35 | +23 | +24 | +23 | +24 | +23 |
| +23.00 | +23 | +23 | +23 | +23 | +23 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| −23.00 | −23 | −23 | −23 | −23 | −23 |
| −23.35 | −24 | −23 | −23 | −24 | −23 |
| −23.50 | −24 | −23 | −23 | −24 | −23 or −24 |
| −23.67 | −24 | −23 | −23 | −24 | −24 |
The way you round can really change the final answer if you do many calculations. For example, in 1982, the Vancouver Stock Exchange created a new stock index. It started at 1000.000. After 22 months, it seemed to have dropped to about 520. But stock prices had actually gone up! The problem was that the index was rounded down thousands of times a day. These small rounding errors added up. When they recalculated with better rounding, the index was actually 1098.892.
What to do when a number is exactly in the middle?
When you round to the nearest whole number, what do you do if the number is exactly halfway between two whole numbers? For example, what about 23.5? This is where "tie-breaking" rules come in.
Round half up
This rule is very common. If the number ends in .5, you always round up.
- If the decimal part is exactly 0.5, then you add 0.5 to the number.
For example, 23.5 becomes 24. But -23.5 becomes -23. This rule is often taught in elementary schools.
This rule is not perfectly balanced. Numbers ending in .5 always round up. This can cause a small positive bias (a slight leaning towards higher numbers) in the results.
Round half down
This rule is the opposite of "round half up." If the number ends in .5, you always round down.
- If the decimal part is exactly 0.5, then you subtract 0.5 from the number.
For example, 23.5 becomes 23. And -23.5 becomes -24. This rule also creates a bias, but it's a negative bias (a slight leaning towards lower numbers).
Round half away from zero
This rule rounds numbers ending in .5 away from zero.
- If the decimal part is exactly 0.5, you round up if the number is positive. You round down if the number is negative.
For example, 23.5 becomes 24. And -23.5 becomes -24. This method is balanced if you have an equal number of positive and negative values. It's often used for money conversions because it's easy to understand.
Round half towards zero
This rule rounds numbers ending in .5 towards zero.
- If the decimal part is exactly 0.5, you round down if the number is positive. You round up if the number is negative.
For example, 23.5 becomes 23. And -23.5 becomes -23. This method is also balanced for positive and negative numbers.
Round half to even
This is a very fair tie-breaking rule.
- If the decimal part of your number is 0.5, you round to the even whole number that is closest.
So, +23.5 becomes +24 (because 24 is even). +22.5 becomes +22 (because 22 is even). -22.5 becomes -22. And -23.5 becomes -24.
This method is balanced for both positive and negative numbers. It also helps keep the average value of rounded numbers close to the original average. This rule is sometimes called "bankers' rounding" and is used a lot in accounting. It's also the default rounding method used in many computer calculations.
Round half to odd
This rule is similar to "round half to even."
- If the decimal part of your number is 0.5, you round to the odd whole number that is closest.
So, +22.5 becomes +23 (because 23 is odd). +21.5 becomes +21 (because 21 is odd). -21.5 becomes -21. And -22.5 becomes -23. This method is rarely used.
Stochastic rounding
This is a less common but very fair tie-breaking method.
- If the decimal part of your number is 0.5, you randomly choose to round up or down. There's an equal chance of either happening.
This rule is very balanced. But it means that if you do the same calculation twice, you might get slightly different results because of the random choice.
Alternating tie-breaking
This method is a bit unusual.
- If the decimal part is 0.5, you alternate between rounding up and rounding down. For example, the first time you see a .5, you round up. The second time, you round down.
This method avoids randomness, but it can still cause a bias if you have an odd number of .5 values.
Rounding in computers
In computers, numbers are often stored in a special way called "floating-point arithmetic." This means numbers are stored with a specific number of important digits. When a computer rounds, it aims to turn a number into one with a certain number of these "significant" digits. The way it rounds depends on the size of the number.
Computers usually follow the same rounding rules we discussed earlier. The IEEE 754 standard is a set of rules that most computer manufacturers follow. This standard lets users choose different rounding methods. It also explains exactly how numbers should be rounded. This makes computer calculations more predictable.
Double rounding
Sometimes, a number might be rounded twice. For example, rounding 9.46 to one decimal place gives 9.5. Then, rounding 9.5 to a whole number using "round half to even" gives 10. But if you rounded 9.46 directly to a whole number, you might get 9.
Some computer rules say that numbers shouldn't be rounded twice in a row in simple calculations. This helps keep results accurate.
The table-maker's dilemma
A computer scientist named William Kahan came up with the term "The Table-Maker's Dilemma." It describes how hard it is to correctly round results for very complex math functions.
For example, it's hard to know exactly how many extra digits you need to calculate to make sure you round a complex math problem perfectly. Even knowing if a finite number of extra digits will be enough can be a very difficult math problem!
The IEEE floating-point standard guarantees that basic math operations (like adding, subtracting, multiplying, dividing, and square roots) will give correctly rounded results. But for more complex functions, there's no such guarantee. They are usually only accurate to the very last digit.
Some special computer programs can now give perfectly accurate results for these complex functions.
History of rounding
The idea of rounding is very old. It might even be older than the idea of division! Ancient clay tablets from Mesopotamia show tables with rounded numbers. People in ancient times also used rounded numbers for things like π and the length of the year.
The "round-to-even" method has been a standard in the U.S. since 1940. It was also known as "the computer's rule" in the early 1900s, meaning human calculators used it for math tables. The term "bankers' rounding" is a bit of a mystery. It's not clear if banks actually used this method as a standard. In fact, a European report on the euro said there was no standard rounding method in banking before and suggested rounding half-way amounts up.
Before the 1980s, how computers rounded numbers was often a secret. It was different for every computer. This changed when the IEEE 754 standard was created. This standard made computer math much more reliable and consistent.
Rounding in programming
Most programming languages have special tools or functions to round numbers. Older languages often only rounded by cutting off the decimal part (rounding towards zero). If you wanted other types of rounding, you had to write your own code for it. For example, to round a positive number to the nearest whole number, you might add 0.5 and then cut off the decimal.
Today, most languages offer at least four basic rounding functions: round up, round down, round to nearest, and round towards zero. How they handle numbers exactly in the middle can vary. Many languages follow the IEEE-754 standard. Some languages can even round a number to a specific number of decimal places, like changing 4321.5678 to 4321.57.
Other rounding rules
Some groups or industries have their own specific rules for rounding.
U.S. Weather Observations
In 1966, the U.S. Office of the Federal Coordinator for Meteorology decided that weather data should be rounded to the nearest whole number. They used the "round half up" rule for tie-breaking. So, 1.5 would become 2, and -1.5 would become -1. Before this, they used "round half away from zero."
Negative zero in meteorology
Some meteorologists might write "-0" for a temperature. This means the temperature was between 0.0 and -0.5 degrees, and it was rounded to zero. They use this when the negative sign is important, like when talking about temperatures below freezing in Celsius.
See also
 In Spanish: Redondeo para niños
In Spanish: Redondeo para niños
 | Madam C. J. Walker |
 | Janet Emerson Bashen |
 | Annie Turnbo Malone |
 | Maggie L. Walker |