Spherical geometry facts for kids
.jpg)
Spherical geometry is a special type of geometry that studies shapes and figures on the surface of a sphere. Imagine drawing on a ball instead of a flat piece of paper! This kind of geometry is very useful for things like making maps of the Earth or charting the positions of stars in the sky.
It's different from the Euclidean geometry you might learn in school, which is always about flat surfaces. Spherical geometry is also a type of Non-Euclidean geometry.
In spherical geometry, a point is just a specific spot on the sphere. But a "straight line" is a bit different. On a sphere, the shortest path between two points is actually a curved line called a "great circle arc." Think of the equator on a globe – that's a great circle! Some rules (theorems) from flat geometry don't work on a sphere, but many have been changed to fit.
Contents
What is Spherical Geometry?
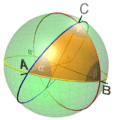
Spherical geometry explores how shapes behave on a curved surface. Unlike a flat plane, a sphere has constant curvature. This means that if you draw a triangle on a sphere, the sum of its angles will always be greater than 180 degrees. This is a key difference from Euclidean geometry.
How are Points and Lines Defined?
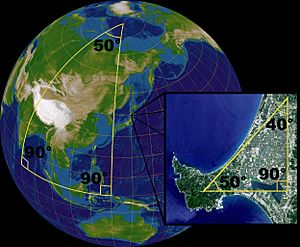
In spherical geometry, a point is simply a location on the surface of the sphere. What we call a "straight line" is actually the shortest path between two points on the sphere's surface. This path is part of a great circle. A great circle is the largest circle you can draw on a sphere. It divides the sphere into two equal halves. For example, the equator and lines of longitude on Earth are great circles.
Why is it Different from Flat Geometry?
Flat, or Euclidean, geometry works on a flat surface where lines are truly straight and parallel lines never meet. On a sphere, parallel lines don't exist in the same way. If you draw two "straight lines" (great circles) that start parallel, they will eventually meet at two points on the opposite sides of the sphere. This difference makes many of the familiar rules of Euclidean geometry change when applied to a sphere.
Uses of Spherical Geometry
Spherical geometry has been important for centuries. It helps us understand our world and the universe around us.
Mapping the Earth and Stars
One of the first uses of spherical geometry was in cartography, the art of making maps. Since the Earth is a sphere (or close to it), understanding spherical geometry is crucial for accurately representing its surface on a flat map. It's also used in astronomy to plot the positions of stars and planets, as they appear on the celestial sphere.
Pilots and sailors use principles of spherical geometry for navigation. The shortest path between two points on Earth is often a great circle route. This is why flights between distant cities might appear curved on a flat map but are actually the most direct path over the globe.
Images for kids
-
A sphere with a spherical triangle drawn on its surface.
See also
In Spanish: Geometría esférica para niños
