Theorema Egregium facts for kids
Gauss's Theorema Egregium is a Latin phrase that means "Remarkable Theorem." It was discovered by a brilliant mathematician named Carl Friedrich Gauss in 1827. This theorem is a big idea in a field of math called differential geometry, which studies shapes and surfaces.
The theorem talks about something called Gaussian curvature. Imagine a surface, like a ball or a piece of paper. Gaussian curvature describes how much that surface is curved at any point.
What makes Gauss's theorem so remarkable? It says you can figure out a surface's Gaussian curvature just by measuring things on the surface itself. You don't need to know how the surface is placed in 3D space.
Think of it this way: if you can bend a surface without stretching or tearing it, its Gaussian curvature won't change. This means the curvature is a special quality that belongs to the surface itself, no matter how you bend it.
Gauss himself explained it like this (translated from Latin):
If a curved surface is developed upon any other surface whatever, the measure of curvature in each point remains unchanged.
This theorem is "remarkable" because the original way we define Gaussian curvature depends on how the surface sits in space. So, it's a big surprise that the curvature doesn't change even when you bend and twist the surface!
In modern math language, the theorem means:
The Gaussian curvature of a surface stays the same if you bend it without stretching.
Contents
Everyday Examples of Theorema Egregium
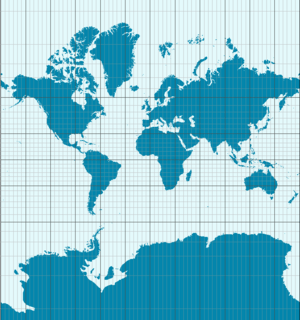
Why Maps Are Tricky
Let's think about a sphere, like a ball. A sphere has a constant Gaussian curvature. Now, think about a flat surface, like a piece of paper. A flat surface has zero Gaussian curvature.
Because of Theorema Egregium, you can't flatten a ball perfectly onto a piece of paper without stretching or tearing it. Try to flatten an empty eggshell – its edges will crack! In the same way, you can't perfectly wrap a flat piece of paper around a ball without crumpling it.
This is super important for cartography, which is the art of making maps. Since Earth is roughly a sphere, you can't make a perfectly flat map of it without distorting distances or shapes. Every map projection has to stretch or squish some parts of the Earth.
Pizza and Corrugated Cardboard
Have you ever wondered why bending a slice of pizza makes it easier to eat? A flat slice of pizza has zero Gaussian curvature. When you gently fold it along the middle, you're bending it without really stretching it.
This bending creates stiffness in the direction perpendicular to the fold. It helps the pizza slice hold its shape so you can eat it without a mess!
This same idea is used in construction and everyday items. Think about corrugated materials, like corrugated fiberboard (cardboard boxes) or corrugated galvanised iron (wavy metal roofs). The waves or folds make these materials much stronger and more rigid than if they were just flat sheets. This is because the bending changes how the material resists forces, thanks to Gauss's Remarkable Theorem!
See also
- Gaussian curvature
- Carl Friedrich Gauss
