Alyutor language facts for kids
Quick facts for kids Alyutor |
||||
|---|---|---|---|---|
| алуталг’у alutalg'u |
||||
| Native to | Russia | |||
| Region | Kamchatka | |||
| Ethnicity | Alyutors | |||
| Native speakers | 25 (2010 census)e18 | |||
| Language family |
Chukotko-Kamchatkan
|
|||
| Dialects |
Alutor
Palana Koryak
|
|||
| Writing system | Cyrillic script | |||
| Official status | ||||
| Official language in | Tigilsky District, Karaginsky District, Kamchatka (Russia) | |||
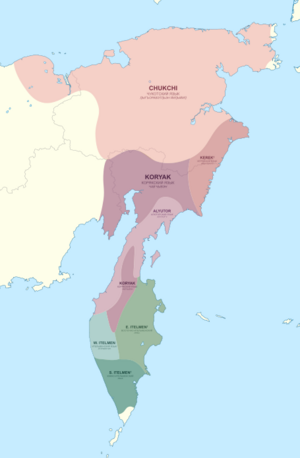
Pre-contact distribution of Alyutor (light purple) and other Chukotko-Kamchatkan languages
|
||||

|
||||
|
||||
Alyutor is a special language spoken in Russia. It belongs to a group of languages called Chukotko-Kamchatkan languages. The Alyutors people speak it. Sadly, very few people speak Alyutor today. In 2010, only about 25 speakers were counted. This means it is a language that is in danger of disappearing.
Contents
The Alyutor Language Today
The Alyutor people are the original inhabitants of the northern part of the Kamchatka Peninsula in Russia. For a long time, the Alyutor language was not written down. It was also considered a "village" version of the Koryak language. However, Alyutor is actually quite different from the Koryak language spoken by nomadic groups. The word "Alyutor" itself means "villager."
In the 1970s, most young people in the main Alyutor village of Vyvenka did not learn the language. This made it even more endangered. But there is good news! In recent years, the school in Vyvenka village has started teaching Alyutor. This helps keep the language alive for future generations.
How Alyutor Sounds
Vowels and Consonants
Alyutor has six different vowel sounds. Five of these vowels can be either long or short. One special vowel, called a schwa (like the 'a' in 'about'), is always short.
The language also uses 18 different consonant sounds.
Word Stress
In Alyutor words, the stress (the part you say with more emphasis) usually falls on the second syllable if the word has many syllables. For words with two syllables, the stress is usually on the first syllable.
For example, words like 'water', 'skin', 'to feed', 'husband', and 'mukluk' follow this rule.
If a syllable has a schwa vowel and is at the beginning of a two-syllable word, the stress moves to the last syllable. Then, a new, extra syllable is sometimes added at the end. For example, a word that might have sounded like *'mosquito' changes to 'mosquito'.
The very last syllable of a word is never stressed.
Syllable Rules
Every syllable in Alyutor begins with a single consonant. If a vowel is short (including the schwa), the syllable can also end with a single consonant. You won't find groups of consonants at the very beginning or end of words. If a word would normally have a tricky consonant group, a schwa vowel is often added to break it up.
Words in Alyutor always end exactly where a syllable ends. This makes the language sound very clear.
How Alyutor is Written
The Alyutor language does not have one official way of writing it down. However, a newspaper called Aborigen Kamchatki uses a specific Cyrillic alphabet to write Alyutor words. This alphabet helps people read and write in Alyutor.
| А а | Б б | В в | Вʼ вʼ | Г г | Гʼ гʼ | Ғ ғ | Д д |
| Е е | Ә ә | Ё ё | Ж ж | З з | И и | Й й | К к |
| Ӄ ӄ | Л л | М м | Н н | Ӈ ӈ | О о | П п | Р р |
| С с | Т т | У у | Ф ф | Х х | Ц ц | Ч ч | Ш ш |
| Щ щ | Ъ ъ | Ы ы | Ь ь | Э э | Ю ю | Я я |
How Alyutor Works
Alyutor is a polysynthetic language. This means that many parts of a sentence can be combined into one very long word. It's like building a super-word that carries a lot of meaning!
For example, in Alyutor, you might say:
ɣəmmə
I.ABS
t-ə-plak+tavamjat-ə-tkən
1SG.S-E-boot+crumple-E-IMPERF
'I soften boots '
This single word means "I soften boots."
The language also uses agglutinative features. This means it adds many small pieces (like prefixes and suffixes) to words to change their meaning. These pieces are like building blocks that stick together.
For example:
qəlʲippə
bread+NOM+SG
tətu-kki
eat.with.something-CVB
ɣeqə⟩masla⟨ta
ASSOC⟩butter⟨ASSOC
n-ə-mal-qin.
good
'Bread (eaten) with butter is excellent.'
Here, you can see how different parts are added to the words to create the full meaning.
Alyutor uses an ergative system. This is a special way that languages mark the "doer" of an action. In simple terms, how a noun is marked depends on whether it's the subject of a simple action or the subject of an action that affects something else.
For example:
ən-an(nə)
he-ERG
ɣəmmə
me+ABS
ina-ɣal-i.
1SG.P-walk.past-3SG.A
'He walked past me.'
Here, "he" is marked differently because he is the one doing the walking.
The order of words in Alyutor sentences can change a lot. It's hard to say there's one "normal" word order. However, sentences where the verb comes first, followed by the object, are quite common.
Here are some examples of how word order can look:
tita·qa
once
qutkinʲnʲaqu-nak
(name)-ERG+SG
maŋ.ki·ʔana
somewhere
ɣa⟩laʔu⟨lin
RES⟩see⟨RES+3SG.P
ʔənnə-ʔən.
fish-ABS+SG
'Once Qutkinnyaqu saw a fish somewhere.'
ɣa⟩nvə⟨lin
RES⟩poke⟨RES+3SG.P
qutkinʲnʲaqu-nak
(name)-ERG+SG
təlɣə-lŋən
finger-ABS+SG
ŋan.tiŋ.
there
'Qutkinnyaqu stuck his finger there.'
Word Forms and Changes
Alyutor words change their form depending on how they are used in a sentence. This is called morphology. Alyutor has different types of words, like nouns (names of things), adjectives (describing words), numbers, pronouns (like 'he' or 'she'), verbs (action words), and more.
Nouns
Nouns in Alyutor change based on their grammatical number (singular, dual, or plural) and their grammatical case. Case tells you the role of the noun in the sentence (e.g., who is doing the action, who is receiving it).
Alyutor has three numbers:
- Singular: for one thing.
- Dual: for two things (this is special, many languages only have singular and plural).
- Plural: for more than two things.
There are eleven different cases in Alyutor! These include:
- Absolutive: The basic form of the noun, often used for the subject of a simple sentence or the object of an action.
- Ergative: Used for the "doer" of an action that affects something else.
- Locative: Shows location or direction.
- Dative: Used for the receiver of something or the goal of an action.
- Lative: Shows movement towards a goal.
- Prolative: Shows movement along or from something.
- Equative: Means "like X" or "as X."
- Contactive: Used for objects that touch something.
- Causative: Shows what causes an action.
- Comitative: Means "with" someone or something (usually living things).
- Associative: Also means "with," but for things that are not living or are less active.
These cases and numbers are usually shown by adding a single ending to the word. Sometimes, a special kind of ending called a circumfix (which goes around the word) is used.
How Nouns Change for People
Nouns can also change to show if they refer to "I" (first person) or "you" (second person). These special endings are added only when the noun is in its basic (absolutive) form.
- For "I" (first person): -j-ɣəm (singular), -muri (dual), -muru (plural)
- For "you" (second person): -j-ɣət (singular), -turi (dual), -turu (plural)
For example:
- ...ʡopta am-ʡujamtawilʔ-ə-muru means "yes we the people"
- japl=q ʡujamtawilʔ-iɣəm means "and I'm a man"
Numbers in Alyutor
Alyutor has simple words for the numbers one to five, ten, and twenty. For all other numbers, they combine these basic words.
- ənnan - one
- ŋitaq - two
- ŋəruqqə - three
- ŋəraqqə - four
- məlləŋin - five
- ənnanməlləŋ(in) - six (which means "one-five")
- ŋitaqməlləŋ(in) - seven (which means "two-five")
- ŋəruqməlləŋ(in) - eight (which means "three-five")
- ŋəraqməlləŋ(in) - nine (which means "four-five")
- mənɣətkin - ten
- mənɣətək ənnan - eleven (which means "ten one")
- qəlikkə - twenty (which means "a score")
- qəlikək ənnan - twenty one (which means "twenty one")
- ŋəraqmənɣətkin - forty (which means "four tens")
- ŋəraqmənɣətkin ŋəraqqə - forty four (which means "four tens four")
- ŋitaqməlləŋin mənɣətkin - seventy (which means "seven tens")
- mənɣətək mənɣətkin - hundred (which means "ten tens")
Verbs
Verbs are action words. In Alyutor, verbs can be either "finite" (meaning they change based on who is doing the action) or "non-finite" (meaning they don't change as much).
How Verbs Change
Finite verbs in Alyutor change to match the person and number of the people or things involved in the action. If a verb describes an action done by one person, it changes to match that person. If it describes an action done by two people, it changes for both.
Verbs also show two main aspects:
- Perfective: This is the basic form of the verb, showing an action that is completed.
- Imperfective: This uses an ending like -tkə / -tkəni to show an ongoing or repeated action.
Alyutor verbs also have five different moods, which show the speaker's attitude or intention:
- Indicative: For facts or statements.
- Imperative: For commands.
- Optative: For wishes or desires.
- Potential: For actions that might happen.
- Conjunctive: For actions connected to other actions.
Other Verb Forms
Some verbs in Alyutor are "monopersonal," meaning they only change for one person, usually the third person (he/she/it). Other verbs are "impersonal," meaning they don't refer to a specific person at all.
Non-finite verb forms include:
- Infinitive: The basic form of the verb (like "to run").
- Supine: A special form used to show purpose.
- Gerunds: Verb forms that act like adverbs.
- Participles: Verb forms that act like adjectives.

