Closure (mathematics) facts for kids

In mathematics, closure is a cool idea that describes when a math operation always gives you a result that belongs to the same group of numbers you started with. Think of it like this: if you have a special club of numbers, and you do something to two numbers from that club, the answer should still be in the club. If it is, then the club is "closed" for that operation!

For example, let's look at real numbers (these are all the numbers you usually think of, like 1, 2.5, -3, or even pi).

• When you add two real numbers, the answer is always another real number. So, addition has closure for real numbers.
• The same is true for multiplication. Multiply any two real numbers, and you'll get another real number.

But not all operations have closure!

• Division does not have closure for real numbers, because you can't divide by zero. If you try to divide a number by 0, the answer isn't a real number.
• Consider natural numbers (these are 1, 2, 3, and so on, no negatives or fractions). If you subtract two natural numbers, the answer might not be a natural number. For example, 3 - 5 = -2, and -2 is not a natural number. So, subtraction does not have closure for natural numbers.
• However, if you look at integers (which include natural numbers, zero, and negative whole numbers like -1, -2, -3), subtraction *does* have closure. If you subtract any two integers, the answer will always be another integer.

Making Sets "Closed"

Sometimes, we can make a group of numbers "closed" for an operation by adding new types of numbers to it. It's like expanding the club so that all the results can fit in.

• We can make the natural numbers closed for subtraction by adding negative numbers and zero. This creates the integers. Now, 3 - 5 = -2, which is an integer.
• We can make rational numbers (numbers that can be written as fractions, like 1/2 or 3/4) closed for operations like finding square roots. If you add numbers like the square root of 2 (which can't be written as a simple fraction), you get the real numbers.
• And if you want to find the square root of negative numbers, you need to add even more numbers! By including square roots of negative numbers (like the square root of -1), you get the complex numbers. These numbers are so powerful that you can find a root for any non-zero polynomial equation within them. Mathematicians show this relationship as .

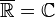Related pages

• Group (mathematics)