Coprime integers facts for kids

Two integers are called coprime, relatively prime, or mutually prime if the only positive integer that divides both of them is 1. This means they don't share any common factors other than 1. For example, the numbers 8 and 9 are coprime. Even though neither 8 nor 9 is a prime number by itself, their only common divisor is 1.

On the other hand, 6 and 9 are not coprime. This is because both 6 and 9 can be divided by 3. When you have a fraction that is fully simplified, like 2/3, the top number (numerator) and the bottom number (denominator) are always coprime.

How to Check if Numbers are Coprime

When two integers, let's call them a and b, are coprime, we often write it using a special math notation. We say their greatest common divisor (GCD) is 1. This looks like gcd(a, b) = 1.

A quick way to find out if two numbers are coprime is by using the Euclidean algorithm. This is a clever method to find the greatest common divisor of two numbers. If the GCD turns out to be 1, then the numbers are coprime!

The number of integers that are coprime with a positive integer n (and are between 1 and n) can be found using something called Euler's totient function. It's written as φ(n).

Important Facts About Coprime Numbers

• The numbers 1 and -1 are special. They are coprime with every other integer.
• If two numbers are coprime, it means no prime number can divide both of them. For example, 8 is divisible by 2, and 9 is divisible by 3. No prime number divides both 8 and 9.
• There's a cool math rule called Bézout's identity. It says that if a and b are coprime, you can always find two other integers, x and y, so that ax + by = 1.
• If a and b are coprime, their least common multiple (LCM) is simply their product. So, lcm(a, b) = ab. For example, the LCM of 8 and 9 is 72 (8 x 9).
• If a and b are coprime, then any powers of these numbers, like a^k and b^m, will also be coprime.
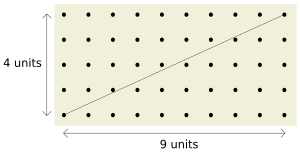
• Imagine plotting two numbers a and b as a point (a, b) on a graph. These two numbers are coprime if you can draw a straight line from the origin (0,0) to the point (a, b) without hitting any other points with whole number coordinates along the way. Look at Figure 1 to see this idea!

Figure 1. The numbers 4 and 9 are coprime. This means a line from (0,0) to (4,9) doesn't pass through any other grid points.

Coprime Sets of Numbers

Sometimes, we talk about a whole set of integers being coprime. This means that the greatest common divisor of *all* the numbers in the set is 1. For example, the numbers 6, 10, and 15 are coprime as a set because 1 is the only positive integer that divides all three of them.

There's also a stronger idea called pairwise coprime. This means that *every pair* of different numbers in the set is coprime.

• The set {2, 3, 4} is coprime (because the GCD of 2, 3, and 4 is 1).
• However, {2, 3, 4} is *not* pairwise coprime. Why? Because 2 and 4 are not coprime (their GCD is 2, not 1).

Pairwise coprimality is very important in number theory, especially for things like the Chinese remainder theorem.

How Likely Are Two Random Numbers to Be Coprime?

If you pick two numbers randomly, what's the chance they will be coprime? It turns out the probability is about 61%! More precisely, it's 6/π². This number comes from advanced math involving prime numbers and something called the Riemann zeta function.

Generating Coprime Pairs

You can actually create all pairs of positive coprime numbers using a special method! Imagine a tree that starts with the pair (2, 1) or (3, 1). From any pair (m, n), you can generate three new coprime pairs:

• Branch 1: (2m-n, m)
• Branch 2: (2m+n, m)
• Branch 3: (m+2n, n)

This method creates every possible coprime pair without repeating any.

This image shows how coprime pairs can be generated like branches on a tree. The starting point (2,1) is red, and its "children" are orange, then yellow, and so on.

Real-World Uses of Coprime Numbers

Coprime numbers might seem like a math concept, but they have practical uses!

• In machine design, especially with gears, engineers often choose the number of teeth on two meshing gears to be coprime. This helps the gears wear down evenly over time.
• In old cryptography machines, like some Vernam cipher machines or rotor machines, different parts would have different lengths or numbers of teeth. These lengths were often chosen to be pairwise coprime. This made the codes much harder to break because the patterns would repeat only after a very long time.

More About Coprime Ideas

The idea of "coprime" isn't just for integers. It can be used for other math structures too. For example, polynomials (which are like math expressions with variables and powers) can also be called coprime if their greatest common divisor is 1.

See also

• Euclid's orchard
• Superpartient number