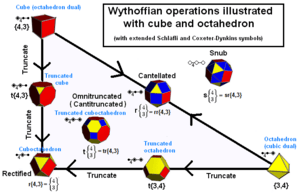
Archimedean solid facts for kids

A truncated icosahedron looks like a soccer ball. It is made of 12 equilateral pentagons and 20 regular hexagons. It has 60 vertices and 90 edges. It is an Archimedean solid

In geometry, an Archimedean solid is a special type of 3D shape called a polyhedron. Imagine a shape made of flat faces, straight edges, and sharp corners. Archimedean solids are unique because:

• Each face is a regular polygon (like a square, triangle, or pentagon where all sides and angles are equal).
• All the corners (called vertices) look exactly the same.
• They are not Platonic solids, prisms, or antiprisms.

There are usually considered to be 13 such shapes. Two of these shapes also have a "mirror image" version, meaning they can't be rotated to look exactly the same as their original. These cool shapes are named after the ancient Greek mathematician Archimedes, who probably found them around 250 BC. His original writings are lost, but other mathematicians later described them. During the Renaissance, artists and mathematicians rediscovered these forms. Johannes Kepler likely finished finding all of them around 1620.

To build an Archimedean solid, you need at least two different types of regular polygons for its faces. For example, a soccer ball (which is a truncated icosahedron) uses both pentagons and hexagons.

What Makes Them Special?

• Equal Edges: Since Archimedean solids are made from regular polygons, all their edges are the same length. This makes them very symmetrical.
• From Platonic Solids: You can often create Archimedean solids by "cutting" or "truncating" the corners or edges of Platonic solids. Platonic solids are even simpler 3D shapes, like a perfect cube or a pyramid with four triangle sides.
• Same Corners: Every corner of an Archimedean solid looks identical. If you stand at any corner and look around, you'll see the same pattern of polygons meeting there.

How They Relate to Platonic Solids

The Archimedean solids can be made by "cutting" Platonic solids, like this example shows.

Archimedean solids are closely related to Platonic solids. Think of Platonic solids as the basic building blocks. By carefully cutting off their corners or edges in a specific way, you can transform them into Archimedean solids. This process is called truncation.

List of Archimedean Solids

Here is a list of the main Archimedean solids:

Image	Name	Faces	Type of Faces	Edges	Vertices
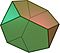	Truncated tetrahedron	8	4 triangles 4 hexagons	18	12
	Cuboctahedron	14	8 triangles 6 squares	24	12
	Truncated cube	14	8 triangles 6 octagons	36	24
	Truncated octahedron	14	6 squares 8 hexagons	36	24
	Rhombicuboctahedron	26	8 triangles 18 squares	48	24
	Truncated cuboctahedron	26	12 squares 8 hexagons 6 octagons	72	48
	Snub cube (2 mirrored versions)	38	32 triangles 6 squares	60	24
	Icosidodecahedron	32	20 triangles 12 pentagons	60	30
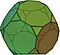	Truncated dodecahedron	32	20 triangles 12 decagons	90	60
	Truncated icosahedron	32	12 pentagons 20 hexagons	90	60
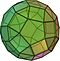	Rhombicosidodecahedron	62	20 triangles 30 squares 12 pentagons	120	60
	Truncated icosidodecahedron	62	30 squares 20 hexagons 12 decagons	180	120
	Snub dodecahedron (2 mirrored versions)	92	80 triangles 12 pentagons	150	60

See also

In Spanish: Sólidos arquimedianos para niños