Platonic solid facts for kids
- The Platonic Solids
A Platonic solid is a special type of three-dimensional shape. It's like a perfect jewel! These shapes have two main rules:
- Every flat side (called a face) is the exact same type of polygon (like a triangle or a square).
- The same number of polygons meet at every single corner of the shape.
There are only five Platonic solids. They are named after the ancient Greek philosopher Plato.
Contents
What Are Platonic Solids?
There are only five unique Platonic solids. Each one is special:
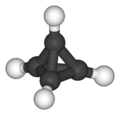
- Tetrahedron: This shape has 4 sides, all made of triangles. It looks a bit like a small pyramid.
- Cube: Also called a Hexahedron, this solid has 6 sides. All its sides are squares. You probably know this one best as a regular dice!
- Octahedron: This shape has 8 sides, and they are all triangles. It looks like two pyramids joined at their bases.
- Dodecahedron: This solid has 12 sides, and each one is a pentagon (a five-sided shape).
- Icosahedron: This shape has 20 sides, and all of them are triangles. It looks like a spiky ball.
The History of Platonic Solids
People have known about Platonic solids for a very long time. Some carved stone balls from ancient Scotland might show these shapes. However, these balls often have rounded bumps, not flat faces.
The ancient Greeks studied these shapes a lot. Some people think the mathematician Pythagoras first discovered them. Others believe that Theaetetus, who lived at the same time as Plato, found the octahedron and icosahedron. Theaetetus was the first to describe all five shapes using math. He also proved that there are only five of them.
Plato's Ideas on Platonic Solids
The Platonic solids are very important in the ideas of Plato. He wrote about them around 360 B.C. in a book called Timaeus. Plato connected each of the four classical elements with a different solid:
- Earth was linked to the cube.
- Air was linked to the octahedron.
- Water was linked to the icosahedron.
- Fire was linked to the tetrahedron.
Plato had reasons for these links. Fire feels sharp, like tiny tetrahedrons. Air feels smooth, like tiny octahedrons. Water flows easily, like tiny round icosahedrons. Earth, made of cubes, is solid and crumbles. The cube is also the only one that can perfectly fill space without gaps.
Plato also mentioned the fifth solid, the dodecahedron. He said that "the god used [it] for arranging the constellations on the whole heaven." Later, Aristotle added a fifth element called aether, which he thought made up the heavens.
Euclid and Kepler's Discoveries
Euclid, another famous Greek mathematician, fully described the Platonic solids. He wrote about them in his famous book, Elements. The last part of his book explains how to build each solid. It also proves that no other perfect, regular shapes exist.
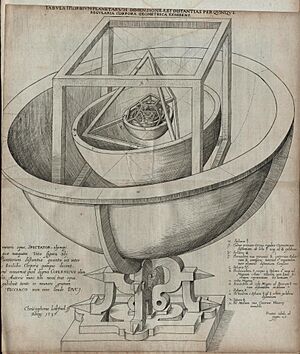
In the 16th century, the German astronomer Johannes Kepler became very interested in these shapes. He tried to connect the five Platonic solids to the five planets known at that time. In his book Mysterium Cosmographicum (1596), Kepler suggested a model of the Solar System. He thought the five solids fit inside each other, separated by spheres. Each sphere represented a planet's orbit.
Kepler believed this arrangement explained the distances between the planets. He placed the octahedron, then the icosahedron, dodecahedron, tetrahedron, and finally the cube. This idea was later proven wrong. However, Kepler's research led to his famous three laws of orbital dynamics. One of these laws states that planets orbit in ellipses, not perfect circles. This changed how people understood physics and astronomy forever.
How Platonic Solids Are Used Today
These shapes are often used to make dice. This is because dice made from these shapes can be very fair. Six-sided dice are common, but other numbers are often used in role-playing games. These dice are usually called D followed by the number of faces, like D8 or D20.
Some Platonic solids are found naturally in crystal structures. The tetrahedron (4 sides), cube (6 sides), and octahedron (8 sides) appear in many crystals. The dodecahedron (12 sides) is similar to a shape found in pyrite crystals.
In meteorology (the study of weather) and climatology (the study of climate), scientists use models based on an icosahedron. These models help predict weather and climate patterns around the world. Using an icosahedron helps avoid problems that happen with other grid systems, especially near the poles.
Images for kids
-
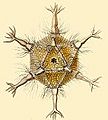
Circogonia icosahedra, a tiny sea creature called a radiolaria, shaped like a regular icosahedron.
See also
 In Spanish: Sólidos platónicos para niños
In Spanish: Sólidos platónicos para niños