Donald Sarason facts for kids
Quick facts for kids
Donald Sarason
|
|
|---|---|

Donald Sarason in January, 2003 at UC Berkeley
|
|
| Born | January 26, 1933 Detroit, Michigan, U.S.
|
| Died | April 8, 2017 (aged 84) Berkeley, California, U.S.
|
| Nationality | American |
| Alma mater | University of Michigan |
| Known for | Hardy space theory and VMO |
| Awards | Sloan Research Fellow, 1969–1971 |
| Scientific career | |
| Fields | Mathematics |
| Institutions | University of California, Berkeley |
| Doctoral advisor | Paul Halmos |
| Doctoral students | Sun-Yung Alice Chang Sheldon Axler Thomas Wolff John Doyle John McCarthy |
Donald Erik Sarason (born January 26, 1933 – died April 8, 2017) was an important American mathematician. He made major discoveries in areas of math known as Hardy space theory and VMO. He was also a very well-liked professor at the University of California, Berkeley. He helped 39 students complete their Ph.D. degrees in mathematics.
Contents
Education and Early Career
Donald Sarason studied at the University of Michigan. He earned his first degree, a Bachelor of Science in Physics, in 1955. He continued his studies there, getting a Master's degree in Physics in 1957. Later, in 1963, he earned his Ph.D. in Mathematics from the same university. His doctoral research was guided by the famous mathematician Paul Halmos.
After finishing his Ph.D., Sarason worked as a postdoctoral researcher. This means he did advanced research after his doctorate. He was at the Institute for Advanced Study from 1963 to 1964. This research was supported by a special grant called a National Science Foundation Postdoctoral Fellowship.
Life at UC Berkeley
In 1964, Donald Sarason joined the University of California, Berkeley as an Assistant Professor. He was promoted to Associate Professor in 1967. By 1970, he became a full Professor. He taught and conducted research at UC Berkeley until he retired in 2012.
Key Achievements
Donald Sarason received a special award called a Sloan Fellowship from 1969 to 1971. This fellowship is given to promising young researchers.
He wrote 78 mathematics papers over 50 years, from 1963 to 2013. He wrote 56 of these papers by himself. The other 22 papers were written with 25 different co-authors.
His work was very influential among other mathematicians. His papers have been mentioned (or "cited") over 4,000 times by other math researchers. This shows how important his ideas were.
Sarason also wrote many reviews for a service called Mathematical Reviews/MathSciNet. These reviews help other mathematicians find and understand new research. He wrote an impressive 456 reviews between 1970 and 2009.
He was also recognized for his teaching skills. The UC Berkeley Mathematics Undergraduate Student Association gave him teaching awards in 2003 and 2006.
At different times, he served on the editorial boards of important math journals. These included Proceedings of the American Mathematical Society, Integral Equations and Operator Theory, and Journal of Functional Analysis. Being on an editorial board means he helped decide which papers would be published.
Important Contributions to Mathematics
Donald Sarason made several significant contributions to the field of mathematics. Here are some of his notable works:
Understanding Functions: Interpolation
- 1967. Generalized Interpolation in
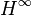 .
.
Sarason found a new way to prove a theorem by G. Pick. This theorem helps solve a problem where you need to find a special function that fits certain conditions. His method connected this problem with another one called the Carathéodory interpolation problem. This work also led to a new way of solving problems in function theory using operator theory.
Exploring Mean Oscillation
- 1975. Functions of Vanishing Mean Oscillation.
Sarason's research was very important for understanding functions on the unit circle in the complex plane. He introduced a new concept called "vanishing mean oscillation" (VMO). Imagine a function that changes value. If its average change over very small sections gets closer and closer to zero, it has vanishing mean oscillation. This idea helped other mathematicians better understand different types of function spaces.
Influential Lecture Notes
- 1978. Function Theory on the Unit Circle.
In 1978, Sarason gave a series of ten lectures at a conference. These lectures were about analytic function theory on the unit circle. He combined older ideas with newer ones from functional analysis. Even though his lecture notes were just a simple printed document, they were shared widely. They became very influential in the field and are still frequently cited by other mathematicians.
New Spaces for Functions
- 1994. Sub-Hardy Hilbert Spaces in the Unit Disk.
This book helped develop the theory of special mathematical spaces called de Branges–Rovnyak spaces. Sarason was a pioneer in studying these spaces in an abstract way. He showed a useful connection between these spaces and certain mathematical operators. His work provided elegant proofs for important theorems like the Julia–Carathéodory and Denjoy–Wolff theorems.
Textbook for Students
- 2007. Complex Function Theory: Second Edition. The American Mathematical Society.
Sarason also wrote a textbook for college students. This book, about complex analysis, gives a very clear introduction to the theory of analytic functions. It's used for advanced undergraduate courses.

