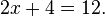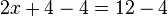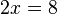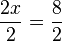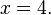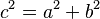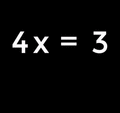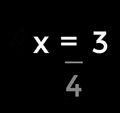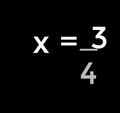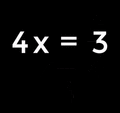Elementary algebra facts for kids
Elementary algebra is a basic type of algebra that students learn. It usually comes after learning arithmetic. In arithmetic, you only work with numbers and symbols like +, −, ×, and ÷. But in algebra, you also use letters called variables (like a, x, or y) to stand for numbers.
Using variables is helpful for a few reasons:
- It lets you solve problems where you don't know a number. This means learning about equations and how to find the missing value (for example, "find x when
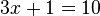 ").
"). - It helps you show general rules from arithmetic. For example, you might know that
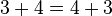 . Algebra helps you prove that
. Algebra helps you prove that 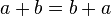 is true for any numbers a and b. This helps you learn about general ideas from many examples.
is true for any numbers a and b. This helps you learn about general ideas from many examples. - It helps you understand how things are related. For example, "if x tickets are sold, the profit will be
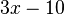 dollars." This shows how profit depends on the number of tickets.
dollars." This shows how profit depends on the number of tickets.
These are the main ideas in elementary algebra. You'll find elementary algebra used in many subjects, like science, business, and building. More advanced algebra, called Abstract algebra, is usually taught much later in college.
Contents
Understanding Algebraic Notation
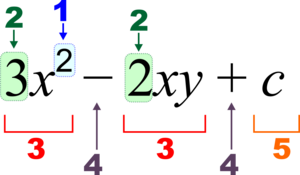
Algebraic notation is simply how algebra is written down. It has special rules and terms. For example, look at the expression 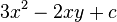 . It has different parts:
. It has different parts:
A coefficient is a number or a letter that stands for a number. It multiplies a variable. For example, in 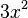 , the number 3 is the coefficient. A term is a part of an expression. It can be a number, a variable, or a mix of both, like
, the number 3 is the coefficient. A term is a part of an expression. It can be a number, a variable, or a mix of both, like 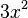 or
or 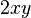 . Terms are usually separated by plus (+) or minus (-) signs.
. Terms are usually separated by plus (+) or minus (-) signs.
Letters are used to represent variables and constants. Usually, letters from the beginning of the alphabet (like 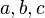 ) are used for constants. These are numbers that don't change. Letters from the end of the alphabet (like
) are used for constants. These are numbers that don't change. Letters from the end of the alphabet (like 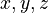 ) are used for variables. These are numbers that can change. They are usually written in italics.
) are used for variables. These are numbers that can change. They are usually written in italics.
Algebraic operations are just like arithmetic operations. These include addition, subtraction, multiplication, division, and exponentiation. They are used with variables and terms. Often, multiplication symbols are left out. For example, 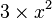 is written as
is written as 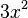 . Also,
. Also, 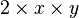 is written as
is written as 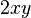 .
.
Usually, terms with the highest power (exponent) are written first. For example, 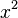 comes before
comes before  . If a coefficient is 1, it's often not written (so
. If a coefficient is 1, it's often not written (so 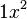 is just
is just 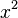 ). If the exponent is 1, it's also not written (so
). If the exponent is 1, it's also not written (so 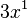 is just
is just 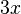 ). If the exponent is 0, the result is always 1 (so
). If the exponent is 0, the result is always 1 (so 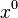 becomes
becomes 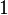 ).
).
Other Ways to Write Algebra
Sometimes, you might see algebraic expressions written differently, especially in computer programs or on calculators. For example, exponents are usually written as small raised numbers, like 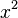 . But in plain text or some computer languages, you might see the caret symbol "^". So,
. But in plain text or some computer languages, you might see the caret symbol "^". So, 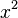 would be written as "x^2".
would be written as "x^2".
In many programming languages, a double asterisk "" is used for exponents. So 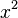 would be "x2". Also, many programming languages and calculators use a single asterisk "*" for multiplication. So,
would be "x2". Also, many programming languages and calculators use a single asterisk "*" for multiplication. So, 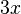 would be written as "3*x".
would be written as "3*x".
Solving Simple Algebra Problems
If an equation has only one unknown number, it can often be easy to solve. Let's call the unknown number "x":
To solve this, you need to get "x" by itself on one side of the equation. You can add, subtract, multiply, or divide both sides of the equation by the same number.
Let's subtract 4 from both sides of the equation:
This gives us:
Now, divide both sides by 2:
And you get:
Key Concepts in Algebra
Variables
Elementary algebra builds on arithmetic by adding letters called variables. These letters stand for numbers that are not specified. This is useful for many reasons:
- Variables can represent numbers you don't know yet. For example, if today's temperature (C) is 20 degrees warmer than yesterday's (P), you can write it as
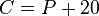 .
. - Variables let you describe general problems. Instead of saying "5 minutes is
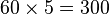 seconds," you can say the number of seconds (
seconds," you can say the number of seconds ( ) is
) is 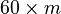 , where
, where 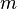 is the number of minutes. This rule works for any number of minutes.
is the number of minutes. This rule works for any number of minutes. - Variables help describe how different amounts are related. For example, the relationship between a circle's circumference (c) and its diameter (d) is
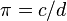 .
. - Variables can show mathematical properties. For instance, a basic rule of addition is that the order of numbers doesn't matter. This is called commutativity. You can write it as
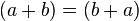 .
.
Working with Expressions
Algebraic expressions can be simplified using basic arithmetic rules.
- When you add the same terms, you can combine them using coefficients. For example,
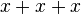 can be simplified to
can be simplified to 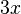 .
. - When you multiply the same terms, you use exponents. For example,
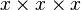 is written as
is written as 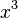 .
. - You can add "like terms" together. For example,
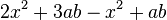 can be simplified to
can be simplified to 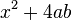 . This is because you add the
. This is because you add the 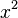 terms together and the
terms together and the 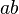 terms together.
terms together. - You can "multiply out" brackets using the distributive property. For example,
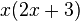 becomes
becomes 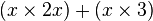 , which simplifies to
, which simplifies to 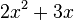 .
. - Expressions can also be "factored." This is like doing the opposite of multiplying out brackets. For example,
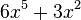 can be written as
can be written as 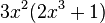 .
.
Equations
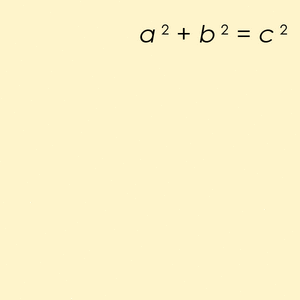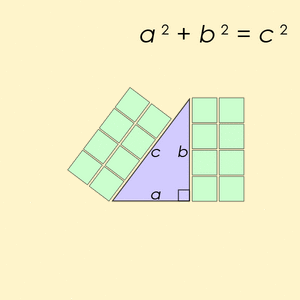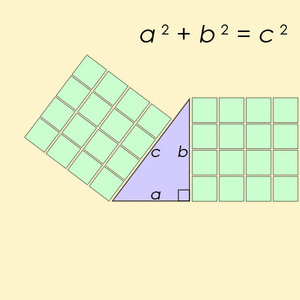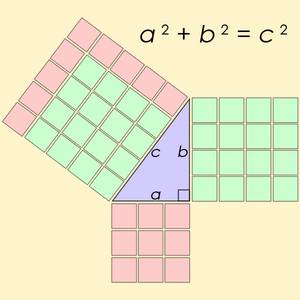
An equation shows that two expressions are equal. It uses the equals sign (=). One famous equation is Pythagoras' law for a right angle triangle:
This equation means that the square of the longest side (called the hypotenuse, c) is equal to the sum of the squares of the other two sides (a and b).
Some equations are true for all values of the variables. These are called identities, like 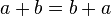 . Other equations are only true for certain values of the variables. For example,
. Other equations are only true for certain values of the variables. For example, 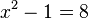 is only true if
is only true if 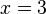 or
or 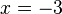 . The values that make an equation true are called its solutions. You find them by equation solving.
. The values that make an equation true are called its solutions. You find them by equation solving.
Another type of equation is an inequality. Inequalities show that one side is greater than or less than the other. The symbols are:
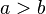 means 'a is greater than b'.
means 'a is greater than b'.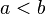 means 'a is less than b'.
means 'a is less than b'.
You can add, subtract, multiply, or divide both sides of an inequality, just like with regular equations. The only special rule is: if you multiply or divide by a negative number, you must flip the inequality symbol. For example, if 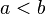 , then
, then 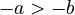 .
.
Rules for Equality
Equality has some important rules:
- Reflexive: Any number is equal to itself (e.g.,
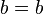 ).
). - Symmetric: If
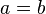 , then
, then 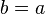 .
. - Transitive: If
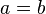 and
and 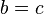 , then
, then 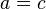 .
.
Also, if two things are equal, you can swap one for the other in any true statement, and the statement will still be true.
- If
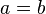 and
and 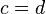 , then
, then 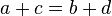 and
and 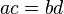 .
. - If
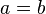 , then
, then 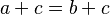 .
. - More generally, if
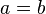 , then
, then 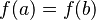 for any function
for any function 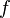 .
.
Rules for Inequality
The relations 'less than' (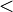 ) and 'greater than' (
) and 'greater than' (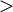 ) also have rules:
) also have rules:
- If
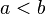 and
and 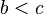 then
then 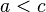 .
. - If
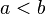 and
and 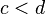 then
then 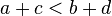 .
. - If
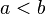 and
and 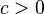 then
then 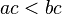 .
. - If
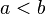 and
and 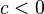 then
then 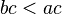 (remember to flip the sign when multiplying by a negative number).
(remember to flip the sign when multiplying by a negative number).
You can also swap the sides of an inequality by flipping the symbol:
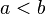 is the same as
is the same as 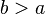 .
.
Substitution
Substitution means replacing a term in an expression with another value or expression. For example, if you have the expression 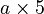 and you substitute 3 for a, you get
and you substitute 3 for a, you get 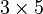 , which means 15.
, which means 15.
If you have a statement that is always true, like a definition, then substituting values into it will also give a true statement. For example, if 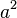 is defined as
is defined as 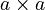 , then substituting 3 for a means
, then substituting 3 for a means 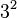 is
is  .
.
Sometimes, you don't know if a statement is always true. Substitution can help you find out what values make it true or false. For example, if you have the statement 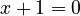 . If you substitute 1 for x, you get
. If you substitute 1 for x, you get 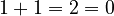 , which is false. This tells you that if
, which is false. This tells you that if 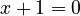 , then x cannot be 1.
, then x cannot be 1.
Images for kids
See also
 In Spanish: Álgebra elemental para niños
In Spanish: Álgebra elemental para niños