Fibonacci sequence facts for kids

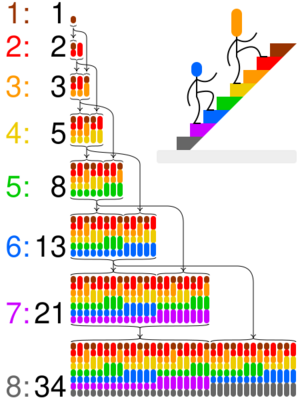
The Fibonacci sequence is a special list of numbers where each number is found by adding the two numbers before it. These numbers are called Fibonacci numbers. The sequence usually starts with 0 and 1.

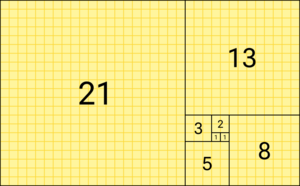
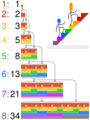
Here's how it begins: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and so on.

This picture shows squares whose sides are Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13, and 21.

The Fibonacci numbers were first noticed in Indian mathematics around 200 BC. They were used to count patterns in Sanskrit poetry. Later, an Italian mathematician named Leonardo of Pisa, also known as Fibonacci, introduced them to Europe in his book Liber Abaci in 1202.

Fibonacci numbers pop up in many unexpected places in mathematics. There's even a whole magazine, the Fibonacci Quarterly, just for studying them! They are used in computer programs, like for searching information or organizing data. They also appear in nature, like how branches grow on trees or how leaves are arranged on a stem. You can see them in the spirals of a pineapple or a pine cone.

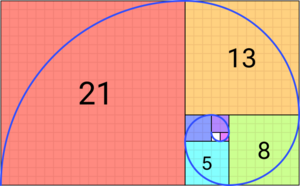
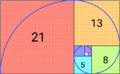
These numbers are also closely linked to the golden ratio. This is a special number that appears often in art and nature. As you go further along the Fibonacci sequence, the ratio of one number to the one before it gets closer and closer to the golden ratio.

What are Fibonacci Numbers?

Fibonacci numbers are defined by a simple rule. You start with 0 and 1. Then, to get the next number, you just add the two numbers before it.

So, if we call the numbers F with a small number next to them (like F₀, F₁, F₂, etc.):

• F₀ = 0
• F₁ = 1
• F_n = F_n-1 + F_n-2 (This means any number F_n is the sum of the two before it: F_n-1 and F_n-2).

The Fibonacci spiral is made by drawing curves inside the Fibonacci squares. It's a close copy of the golden spiral.

Here are the first 20 Fibonacci numbers:

History of the Sequence

In India

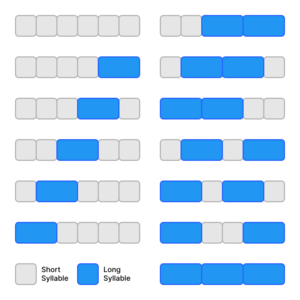
The Fibonacci sequence first appeared in Indian mathematics. It was used to study patterns in Sanskrit poetry. Poets were interested in counting different ways to arrange long and short syllables. A long syllable took 2 units of time, and a short one took 1 unit.

This image shows 13 ways to arrange long and short syllables for a total length of six units.

Counting the patterns for a certain total time led to Fibonacci numbers. For example, if you had 6 units of time, there were 13 ways to arrange the syllables. This knowledge was written down by mathematicians like Pingala (around 450 BC–200 BC) and Hemachandra (around 1150 AD).

In Europe

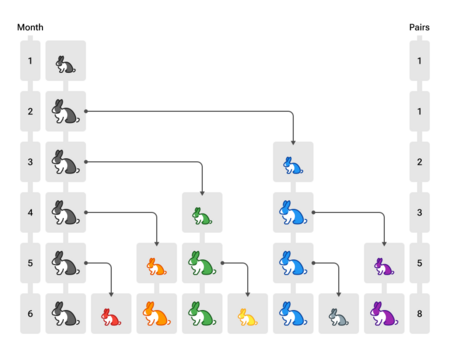
The Fibonacci sequence became known in Europe through Fibonacci's book Liber Abaci (which means 'The Book of Calculation') in 1202. He used it to solve a puzzle about how fast a population of rabbits would grow.

A page from Fibonacci's Liber Abaci. It shows the first 13 Fibonacci numbers, starting with 1, 2, 3, 5, and ending with 377.

Here's the rabbit puzzle:

• Imagine you have one new pair of rabbits.
• Rabbits can mate when they are one month old.
• At the end of their second month, they always have a new pair of rabbits.
• Rabbits never die and keep having babies.

How many pairs of rabbits would there be in one year?

• After 1 month: Still 1 pair (they just mated).
• After 2 months: The first pair has a new pair. So, 2 pairs.
• After 3 months: The original pair has another new pair. The second pair is now one month old and mating. So, 3 pairs.
• After 4 months: The original pair has another new pair. The pair born two months ago also has their first pair. So, 5 pairs.

If you keep going, the number of rabbit pairs each month follows the Fibonacci sequence! The name "Fibonacci sequence" was actually given to it much later by a mathematician named Édouard Lucas in the 1800s.

In this example, the number of rabbit pairs each month follows the Fibonacci sequence. F_n is the number of pairs at the end of month n.

Fibonacci and the Golden Ratio

The golden ratio (often shown by the Greek letter φ, pronounced "phi") is a special number, about 1.618. It's found in many places in nature and art.

One amazing thing about the Fibonacci sequence is how it relates to the golden ratio. If you take any Fibonacci number and divide it by the one before it, the answer gets closer and closer to the golden ratio as you go further along the sequence.

For example:

• 8 / 5 = 1.6
• 13 / 8 = 1.625
• 21 / 13 = 1.615...
• 34 / 21 = 1.619...

As the numbers get bigger, the ratio gets closer to 1.61803... This is the golden ratio!

Cool Math Tricks with Fibonacci Numbers

Divisibility Rules

Fibonacci numbers have some neat patterns when it comes to division:

• Every third Fibonacci number is an even number (a multiple of 2). (F₃=2, F₆=8, F₉=34).
• More generally, if you pick any Fibonacci number F_k, then every F_k-th number in the sequence will be a multiple of F_k. For example, F₄ is 3. So, F₈ (21), F₁₂ (144), etc., are all multiples of 3.
• Any three Fibonacci numbers in a row (like F_n, F_n+1, F_n+2) don't share any common factors other than 1. They are called coprime.

Fibonacci Primes

A Fibonacci prime is a Fibonacci number that is also a prime number. Remember, a prime number is a whole number greater than 1 that has only two divisors: 1 and itself.

The first few Fibonacci primes are: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ...

Scientists have found Fibonacci primes with thousands of digits! But they don't know if there are an endless number of them.

The only Fibonacci numbers that are perfect squares (like 4, 9, 16) are 1 (F₁ and F₂) and 144 (F₁₂).

How Fibonacci Numbers are Used

In Mathematics

You can find Fibonacci numbers by adding up the numbers along the diagonals of Pascal's triangle.

• Pascal's Triangle: You can find Fibonacci numbers hidden in Pascal's triangle. If you add up the numbers along certain diagonals, you get the Fibonacci numbers.
• Climbing Stairs: Imagine you're climbing a staircase. You can take either 1 step or 2 steps at a time. How many different ways can you climb the stairs? The answer is a Fibonacci number! For example, to climb 5 steps, there are 8 ways (which is F₆).

This shows how the Fibonacci sequence can help count ways to climb stairs, taking 1 or 2 steps at a time.

• Binary Strings: Fibonacci numbers also help count certain types of binary codes (strings of 0s and 1s). For example, the number of binary strings of a certain length that don't have two 1s right next to each other is a Fibonacci number.

In Computer Science

• Algorithms: Fibonacci numbers are important in understanding how fast some computer programs work. For example, they help analyze Euclid's algorithm, which finds the greatest common divisor of two numbers.
• Sorting Data: They are used in a special way to sort lists of information, like in a "merge sort" method.
• Optimization: A method called the "Fibonacci search technique" uses these numbers to find the best solution in a problem.
• Planning: Some teams that develop software use a "Modified Fibonacci Series" to estimate how much work a task will take.

In Nature

A Yellow chamomile flower head showing spirals. There are 21 blue spirals and 13 cyan spirals, both Fibonacci numbers. Many plants show these patterns.

Fibonacci numbers appear all over the natural world:

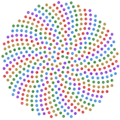
• Plant Growth: You can see them in how branches grow on trees, how leaves are arranged on a stem (called phyllotaxis), and the patterns of seeds in a sunflower head. The spirals on a pineapple or a pine cone often show consecutive Fibonacci numbers.
• Sunflower Spirals: The seeds in a sunflower head grow in spirals. If you count the spirals going one way (clockwise) and then the other way (counter-clockwise), you'll often find that the numbers are consecutive Fibonacci numbers, like 34 and 55, or 55 and 89. This arrangement helps the seeds pack together very efficiently.

This model shows the pattern of florets (small flowers) in a sunflower head.

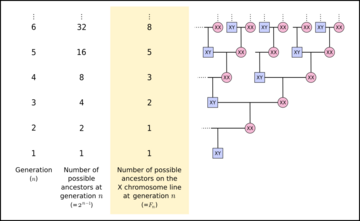
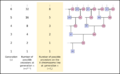
• Bee Family Trees: The family tree of honeybees also follows the Fibonacci sequence. Male bees (drones) hatch from unfertilized eggs, so they only have a mother. Female bees hatch from fertilized eggs, so they have both a mother and a father. If you trace the ancestors of a male bee, you'll find 1 parent, 2 grandparents, 3 great-grandparents, 5 great-great-grandparents, and so on. This is the Fibonacci sequence!
• Human X Chromosome: The number of ancestors who contribute to a person's X chromosome also follows the Fibonacci sequence. A male gets his X chromosome from his mother. His mother got one X from her mother and one from her father. So, the number of ancestors who passed down that X chromosome at each generation is a Fibonacci number.

The number of possible ancestors on the X chromosome inheritance line at each generation follows the Fibonacci sequence.

Other Uses

• Optics: When light passes through two transparent plates, the number of ways it can reflect off the surfaces follows the Fibonacci sequence.
• Financial Markets: Some traders use "Fibonacci retracement levels" in technical analysis to predict price movements in financial markets.
• Art: Artist Mario Merz used the Fibonacci sequence in some of his artworks.

Images for kids

• 

  A tiling with squares whose side lengths are successive Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13 and 21

• 

  The Fibonacci spiral: an approximation of the golden spiral created by drawing circular arcs connecting the opposite corners of squares in the Fibonacci tiling (see preceding image)

• 

  Thirteen (F₇) ways of arranging long and short syllables in a cadence of length six. Eight (F₆) end with a short syllable and five (F₅) end with a long syllable.

• 

  A page of Fibonacci's Liber Abaci from the Biblioteca Nazionale di Firenze showing (in box on right) 13 entries of the Fibonacci sequence: the indices from present to XII (months) as Latin ordinals and Roman numerals and the numbers (of rabbit pairs) as Hindu-Arabic numerals starting with 1, 2, 3, 5 and ending with 377.

• 

  In a growing idealized population, the number of rabbit pairs form the Fibonacci sequence. At the end of the nth month, the number of pairs is equal to F_n.

• 

  The Fibonacci numbers are the sums of the diagonals (shown in red) of a left-justified Pascal's triangle.

• 

  Use of the Fibonacci sequence to count {1, 2}-restricted compositions

• 

  Yellow chamomile head showing the arrangement in 21 (blue) and 13 (cyan) spirals. Such arrangements involving consecutive Fibonacci numbers appear in a wide variety of plants.

• 

  Illustration of Vogel's model for n = 1 ... 500

• 

  The number of possible ancestors on the X chromosome inheritance line at a given ancestral generation follows the Fibonacci sequence. (After Hutchison, L. "Growing the Family Tree: The Power of DNA in Reconstructing Family Relationships".)