Hilbert space facts for kids
A Hilbert space is a special idea in math. Think of it as a type of Euclidean space, but much more general. Euclidean space is what we use to describe the world around us, like a flat paper (two dimensions) or the room you're in (three dimensions). A Hilbert space takes these ideas and lets us explore what happens when there are more than three dimensions, even an infinite number! It's named after a famous mathematician named David Hilbert.
In regular two-dimensional (2D) or three-dimensional (3D) spaces, we use math tools like vector algebra and calculus. Hilbert spaces allow us to use these same powerful tools in spaces with any number of dimensions, whether it's a few or infinitely many. A Hilbert space is a vector space. This means it has a special structure called an inner product. This inner product lets us measure things like the length of a "vector" (like an arrow pointing in a direction) and the angle between two vectors. Also, a Hilbert space must be "complete." This means that all the "paths" or sequences of points that should lead to a specific spot actually do. This completeness is important for calculus to work correctly.
Who Discovered Hilbert Spaces?
The first ideas about Hilbert spaces came out in the early 1900s. Mathematicians like David Hilbert, Erhard Schmidt, and Frigyes Riesz were key in developing these concepts. Later, John von Neumann was the first to use the name "Hilbert Space." These new mathematical tools greatly changed a field of math called functional analysis.
Where Are Hilbert Spaces Used?
Hilbert spaces are very important in many areas. You'll find them in mathematics, physics, and engineering. They are often used to describe spaces with an infinite number of dimensions, especially when dealing with functions.
Here are some places where Hilbert spaces are super useful:
- Solving Equations: They help scientists understand and solve partial differential equations. These equations describe how things change over time and space, like heat flow or wave motion.
- Quantum Mechanics: In quantum mechanics, which studies the tiny world of atoms and particles, Hilbert spaces are essential. They help describe the possible states of particles.
- Fourier Analysis: This area of math breaks down complex signals or waves into simpler parts. It's used in signal processing (like in your phone or computer) and understanding how heat moves.
- Thermodynamics: Hilbert spaces are also part of the math behind thermodynamics. This is the study of heat and energy.
All the normal Euclidean spaces we use every day (like 2D and 3D space) are also types of Hilbert spaces. Other examples include spaces of functions that can be "square-integrated" and spaces of sequences.
Images for kids
-
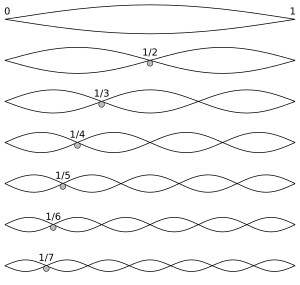
The state of a vibrating string can be modeled as a point in a Hilbert space. The decomposition of a vibrating string into its vibrations in distinct overtones is given by the projection of the point onto the coordinate axes in the space.
-
Completeness means that if a particle moves along the broken path (in blue) travelling a finite total distance, then the particle has a well-defined net displacement (in orange).
-
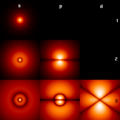
The orbitals of an electron in a hydrogen atom are eigenfunctions of the energy.
See also
In Spanish: Espacio de Hilbert para niños
