Interval arithmetic facts for kids

Interval arithmetic is a special way of doing math on intervals instead of exact numbers. Think of an interval as a range, like "between 5 and 7". This method is mostly used in computers to automatically find and deal with errors.

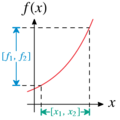
Imagine you have a number you don't know exactly, but you know it's somewhere within a specific range. Interval arithmetic helps you work with that range. If you have a math problem that uses this uncertain number, interval arithmetic will give you a result that is also a range. This new range will definitely contain the true answer.

This technique is useful for handling rounding errors that happen in computer calculations. It also helps with uncertainties from measurements, because every measurement has a small error.

What is Interval Arithmetic?

For numbers that are part of a range (called real intervals), interval arithmetic works like this:

• Adding intervals: When you add two intervals, you add their smallest numbers together and their largest numbers together.

* Example: If you have `[1, 2]` and `[3, 4]`, adding them gives `[1+3, 2+4]`, which is `[4, 6]`. *

• Subtracting intervals: When you subtract one interval from another, you subtract the largest number of the second interval from the smallest number of the first. Then you subtract the smallest number of the second interval from the largest number of the first.

* Example: If you have `[5, 7]` and `[1, 2]`, subtracting them gives `[5-2, 7-1]`, which is `[3, 6]`. *

• Multiplying intervals: To multiply two intervals, you multiply all possible combinations of their end points. The smallest result becomes the start of your new interval, and the largest result becomes the end.

* Example: For `[2, 3]` and `[4, 5]`, you'd check `2*4=8`, `2*5=10`, `3*4=12`, `3*5=15`. The smallest is 8, the largest is 15. So the result is `[8, 15]`. *

• Dividing intervals: Dividing intervals is a bit more complex, especially if the interval you are dividing by includes zero. Generally, you multiply the first interval by the inverse (1 divided by) of the second interval.

* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{[x_1, x_2]}{[y_1, y_2]} = [x_1, x_2] \cdot \frac{1}{[y_1, y_2]} * If the interval `[y_1, y_2]` does not contain zero, then Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{[y_1, y_2]} = \left [\tfrac{1}{y_2}, \tfrac{1}{y_1} \right ] . * If the interval contains zero, the result can be very large, even extending to positive or negative infinity.

How Interval Arithmetic is Used

Interval arithmetic is mainly used in a field called validated numerics. This is where computers need to give answers that are not just close, but are guaranteed to be correct within a certain range. It's also used in other technical areas where precision and error control are important.

Computer Programs for Intervals

Many experts have created computer programs that use interval arithmetic. Some well-known ones include INTLAB (which works with MATLAB), arb, JuliaIntervals, and kv. These programs help scientists and engineers perform calculations with guaranteed accuracy.

Community and Conferences

There are several international meetings where people discuss interval arithmetic. One of the biggest is the International Symposium on Scientific Computing, Computer Arithmetic, and Validated Numerics, often called SCAN. Other workshops like SWIM and REC also bring together researchers to share new ideas.

Images for kids

• 

  Tolerance function (turquoise) and interval-valued approximation (red)

• 

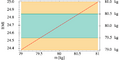
  Body mass index for a person 1.80 m tall in relation to body weight m (in kilograms)

• 

  Body mass index for different weights in relation to height L (in metres)

• 

  Multiplication of positive intervals

• 

  Values of a monotonic function

• 

  Mean value form

• 

  Outer bounds at different level of rounding

• 

  Approximate estimate of the value range

• 

  Treating each occurrence of a variable independently

• 

  Wrapping effect

• 

  Reduction of the search area in the interval Newton step in "thick" functions

• 

  Rough estimate (turquoise) and improved estimates through "mincing" (red)

• 

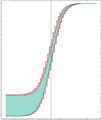
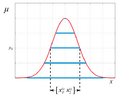
  Approximation of the normal distribution by a sequence of intervals