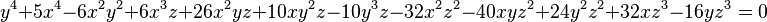Jennifer Balakrishnan facts for kids
Quick facts for kids
Jennifer Balakrishnan
|
|
|---|---|

Jennifer Balakrishnan (2018)
|
|
| Nationality | American |
| Alma mater | |
| Awards |
|
| Scientific career | |
| Fields | Mathematics |
| Institutions | Boston University |
| Thesis | Coleman integration for hyperelliptic curves: algorithms and applications (2011) |
| Doctoral advisor | Kiran Kedlaya |
Jennifer Shyamala Sayaka Balakrishnan is an American mathematician. She is famous for leading a team that solved the problem of the "cursed curve". This was a very difficult math puzzle.
She works on algorithmic number theory and arithmetic geometry. This means she uses computers to solve problems with numbers and shapes. Jennifer Balakrishnan is a professor at Boston University.
Contents
Becoming a Mathematician
Jennifer Balakrishnan was born in Mangilao, Guam. Her father is a chemistry professor. She showed a talent for math from a young age.
Early Achievements
In 2001, when she was in high school, Jennifer won an award. It was for her math project at a big science fair. Her project was about special coordinate systems.
The next year, she won a national calculus competition. This was part of the United States of America Mathematical Olympiad.
University Studies
Jennifer Balakrishnan went to Harvard University. She earned two degrees in mathematics in 2006. She then went to the MIT for her Ph.D. (doctorate degree).
She finished her Ph.D. in 2011. Her main teacher was Kiran Kedlaya. Her research was about solving math problems using special curves.
Postdoctoral Research
After MIT, she continued her research at Harvard. She worked there from 2011 to 2013. Then, she moved to the University of Oxford in England.
At Oxford, she was a research fellow from 2013 to 2016. She worked at Balliol College and the Mathematical Institute.
Teaching at Boston University
In 2016, Jennifer Balakrishnan became a professor at Boston University. She was promoted to a full professor in 2023.
She is also a leader in a big math project. This project involves many universities. These include Boston University, Harvard, and MIT. They work together on number theory and geometry.
Solving the Cursed Curve
In 2017, Jennifer Balakrishnan led a team of mathematicians. They solved the problem of the "cursed curve". This curve is written as a complex equation.
The equation looks like this:
What the Problem Was
The goal was to find all the "rational solutions" to this equation. This means finding numbers for x, y, and z that are fractions or whole numbers. These numbers must make the equation true.
Earlier, other mathematicians had found seven solutions. But they couldn't prove that these were the only solutions. The "cursed curve" was important in the study of elliptic curves.
How They Solved It
Jennifer Balakrishnan's team used a new method. They created a special "Selmer variety" related to the curve. They showed that any solution to the curve must also be on this variety.
By counting the meeting points, they proved that the seven known solutions were indeed the only ones. This big discovery was first shared in 2017. It was later published in a top math journal in 2019.
Jennifer Balakrishnan also works on other math problems. She researches with other mathematicians like Ken Ono. They study questions about special math functions.
She also helps create computer programs for math. These programs are part of the SageMath system. They help mathematicians solve problems.
Awards and Honors
Jennifer Balakrishnan has received many important awards for her work.
- In 2016, she received the Clare Boothe Luce Assistant Professorship.
- In 2018, she was chosen as a Sloan Research Fellow. This is a special award for young scientists.
- In 2020, she won a CAREER Award. This award helps promising researchers.
- In 2022, she became a Fellow of the American Mathematical Society. This honor recognizes her contributions to math.
- Also in 2022, she won the AWM–Microsoft Research Prize in Algebra and Number Theory. This was for her excellent work in solving math problems using explicit methods.
- In 2023, she was named a Fellow of the Association for Women in Mathematics. This was for her support of women in math. She helps mentor students and organizes programs like "Women in Sage".
Selected Publications
- Balakrishnan, Jennifer S.; Bradshaw, Robert W.; Kedlaya, Kiran S (2010). "Explicit Coleman integration for hyperelliptic curves". Algorithmic number theory, 16–31, Lecture Notes in Comput. Sci., 6197, Springer, Berlin.
- Balakrishnan, Jennifer S.; Besser, Amnon (2012). "Computing local p-adic height pairings on hyperelliptic curves". Int. Math. Res. Not. (IMRN), no. 11, 2405–2444.
- Balakrishnan, Jennifer S.; Besser, Amnon; Müller, J. Steffen (2016). "Quadratic Chabauty: p-adic heights and integral points on hyperelliptic curves". J. Reine Angew. Math. 720, 51–79.
- Balakrishnan, Jennifer S.; Dogra, Netan (2018). "Quadratic Chabauty and rational points I: p-adic heights". With an appendix by J. Steffen Müller. Duke Math. J. 167, no. 11, 1981-2038.
- Balakrishnan, Jennifer S.; Dogra, Netan; Müller, J. Steffen; Tuitman, Jan; Vonk, Jan (2019). "Explicit Chabauty-Kim for the split Cartan modular curve of level 13". Ann. of Math. 189, no. 3, 885-944.