Parallel postulate facts for kids
In geometry, the parallel postulate is one of the basic rules, called axioms, of Euclidean geometry. It's sometimes known as Euclid's fifth postulate because it was the fifth rule listed in Euclid's famous book, Elements.
This rule states that if you have a straight line and another point not on that line, you can only draw one straight line through that point that will never cross the first line. Think of two train tracks that run perfectly side-by-side forever.
The type of geometry that follows all of Euclid's original rules is called Euclidean geometry. Geometries that don't follow all of Euclid's rules are known as non-Euclidean geometry.
Contents
Understanding the Parallel Postulate
Euclid's original way of saying the postulate was a bit more complex. It said:
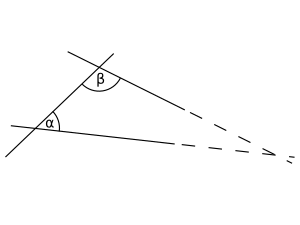
If you have a straight line and two other lines that cross it, and the angles inside those two lines add up to less than 180 degrees (two right angles) on one side, then those two lines will eventually meet if you make them long enough on that side.
This might sound tricky, but it means the same thing as the simpler version. If lines aren't perfectly parallel, they'll eventually cross.
History of the Parallel Postulate
Many mathematicians felt that Euclid's fifth postulate was much longer and harder to understand than his other four basic rules. They thought it should be possible to prove it using the simpler rules. Many tried to prove it, but they all found out they were wrong. Euclid himself was a famous Greek mathematician from Alexandria.
Playfair's Axiom: A Simpler Idea
Later, another mathematician named Playfair came up with a simpler way to state the same idea. It's called Playfair's axiom:
Given a straight line and a point not on this line, you can only draw one straight line through this point that will not meet the other straight line.
Mathematicians discovered that this rule means exactly the same thing as Euclid's original fifth postulate. They are called 'equivalent' because if one is true, the other must also be true. Today, mathematicians often use Playfair's axiom because it's easier to work with.
Exploring Non-Euclidean Geometry
Eventually, some mathematicians decided to try building new types of geometry without using Euclid's fifth postulate. One of these new geometries is called elliptic geometry. In elliptic geometry, the parallel postulate is replaced with a different rule:
Given a straight line and a point not on this line, you cannot draw a straight line through this point that will not eventually cross the other straight line.
When they used this new rule, mathematicians found they could still prove many of Euclid's other theorems. This led to the creation of elliptic geometry.
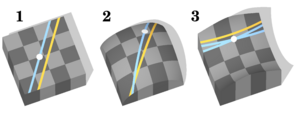
You can imagine elliptic geometry by thinking about the surface of a globe. Lines of longitude (the lines that go from the North Pole to the South Pole) look parallel at the equator. However, they all meet at the poles. This is an example of how lines behave in elliptic geometry.
It was proven that elliptic geometry works perfectly well without contradictions. This showed that Euclid's fifth postulate was truly independent of his other rules. After this, mathematicians stopped trying to prove the fifth postulate. Instead, they started studying other geometries that don't follow Euclid's fifth postulate.
Another rule mathematicians sometimes use instead of Euclid's fifth axiom says:
Given a straight line and a point not on this line, you can draw at least two straight lines through this point that will not eventually cross the other straight line.
This type of geometry is known as hyperbolic geometry.
There's also a geometry that simply removes Euclid's fifth postulate and doesn't replace it with anything. This is called neutral geometry or absolute geometry.
See also
 In Spanish: Quinto postulado de Euclides para niños
In Spanish: Quinto postulado de Euclides para niños