Pentagonal tiling facts for kids

This is the 15th type of pentagon found that can tile a flat surface, discovered in 2015.

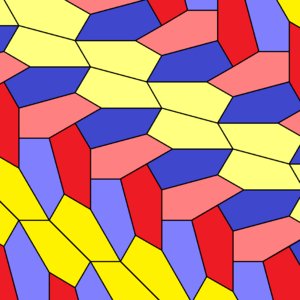
In geometry, a pentagonal tiling is when you cover a flat surface, like a floor, using only shapes that are pentagons. A pentagon is a shape with five straight sides and five angles. This is also called a tiling of the plane.

It's impossible to tile a flat surface using only regular pentagons (where all sides and angles are equal). This is because each angle in a regular pentagon is 108 degrees. You need angles that add up to exactly 360 degrees around a point to tile a surface without gaps or overlaps. Since 108 does not divide evenly into 360, regular pentagons don't work.

However, regular pentagons can tile curved surfaces, like the surface of a sphere or a special type of curved space called the hyperbolic plane.

Finding Pentagons That Tile
Pentagons and Hexagons
Non-Convex Pentagons
Pentagonal Tilings in Different Geometries
Images for kids
See also

Finding Pentagons That Tile

An example pentagon with its angles (A, B, C, D, E) and side lengths (a, b, c, d, e) labeled.

Scientists have found 15 different types of pentagons that can tile a flat surface all by themselves. This means you only need one shape of pentagon to cover the entire surface. The newest type was found in 2015.

In 2017, a mathematician named Michaël Rao said he had proven that these 15 types are the only ones that can tile a flat surface. His proof was checked by other mathematicians and is now widely accepted.

Each of these 15 types of pentagons is unique. However, some pentagons might fit into more than one type. Also, some of these pentagons can create different tiling patterns, not just the main one for their type.

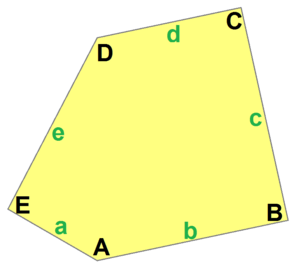
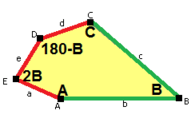
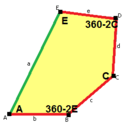
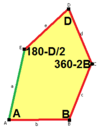
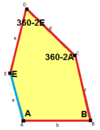
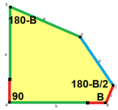
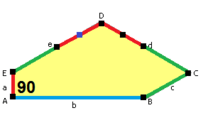
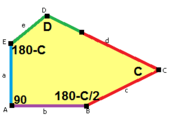
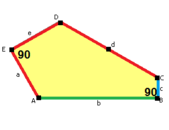
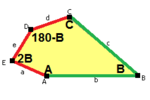
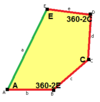
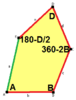
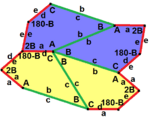
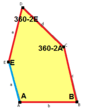
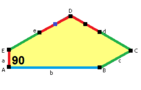
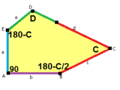
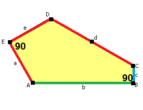
When we talk about the sides and angles of these pentagons:

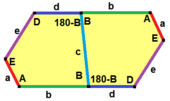
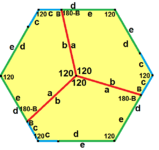
The sides are labeled a, b, c, d, e.
They are measured clockwise from the angles.
The angles are labeled A, B, C, D, E.
Angle A is opposite side d, B is opposite e, and so on.

The 15 Types of Pentagons That Tile
1	2	3	4	5
B + C = 180° A + D + E = 360°	c = e B + D = 180°	a = b, d = c + e A = C = D = 120°	b = c, d = e B = D = 90°	a = b, d = e A = 60°, D = 120°
6	7	8	9	10
a = d = e, b = c B + D = 180°, 2B = E	b = c = d = e B + 2E = 2C + D = 360°	b = c = d = e 2B + C = D + 2E = 360°	b = c = d = e 2A + C = D + 2E = 360°	a = b = c + e A = 90°, B + E = 180° B + 2C = 360°
11	12	13	14	15
2a + c = d = e A = 90°, C + E = 180° 2B + C = 360°	2a = d = c + e A = 90°, C + E = 180° 2B + C = 360°	d = 2a = 2e B = E = 90° 2A + D = 360°	2a = 2c = d = e A = 90°, B ≈ 145.34°, C ≈ 69.32° D ≈ 124.66°, E ≈ 110.68° (2B + C = 360°, C + E = 180°)	a = c = e, b = 2a A = 150°, B = 60°, C = 135° D = 105°, E = 90°

Many of these pentagon types can change their angles and side lengths a bit. This is called having "degrees of freedom."

Tilings often have a repeating pattern, like a wallpaper design. This pattern shows how the tiles are arranged and how they repeat.

A primitive unit is the smallest part of a tiling that can be copied and moved to create the entire pattern.

Early Discoveries (1918)

A mathematician named Reinhardt found the first five types of pentagons that can tile a surface in 1918. All five of these types can create "isohedral" tilings. This means that if you pick any tile in the pattern, you can move or flip the whole pattern so that the chosen tile ends up exactly where another tile was.

There are 24 different ways these first five types of pentagons can tile a surface. Some of these tilings use special versions of the pentagons.

Sometimes, tiles can be "chiral." This means they are mirror images of each other, like your left and right hands. In diagrams, these are often shown in different colors, like yellow and green.

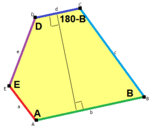
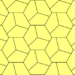
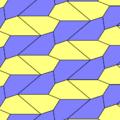
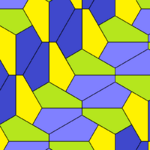
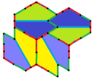
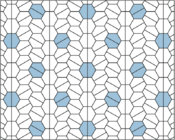
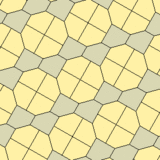
Type 1 Pentagons

Type 1 pentagons are very versatile. They can create many different tiling patterns. Here are some examples:

Tilings of Pentagon Type 1
p2 (2222)	cmm (2*22)	cm (*×)	pmg (22*)	pgg (22×)	p2 (2222)	cmm (2*22)
p2 (2222)	cmm (2*22)	p1 (°)	p2 (2222)	p2 (2222)	p2 (2222)	cmm (2*22)

2-tile primitive unit			4-tile primitive unit
B + C = 180° A + D + E = 360°		a = c, d = e A + B = 180° C + D + E = 360°	a = c A + B = 180° C + D + E = 360°	a = e B + C = 180° A + D + E = 360°	d = c + e A = 90°, 2B + C = 360° C + D = 180°, B + E = 270°

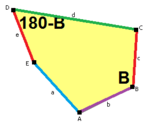
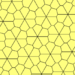
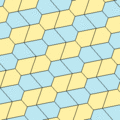
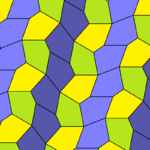
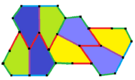
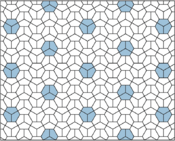
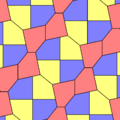
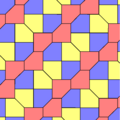
Type 2 Pentagons

These are examples of Type 2 pentagons. They also create isohedral tilings. The second example shows a version where the edges of the pentagons line up perfectly.

Type 2
pgg (22×)
p2 (2222)

4-tile primitive unit
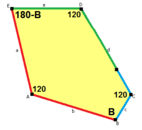
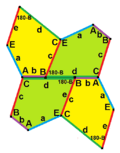c = e B + D = 180°	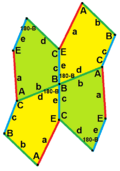c = e, d = b B + D = 180°

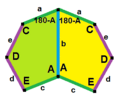
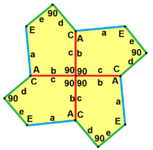
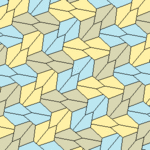
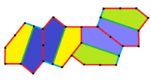
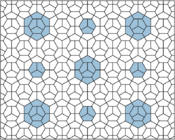
Types 3, 4, and 5 Pentagons

Type 3		Type 4		Type 5
p3 (333)	p31m (3*3)	p4 (442)	p4g (4*2)	p6 (632)


3-tile primitive unit		4-tile primitive unit		6-tile primitive unit	18-tile primitive unit
a = b, d = c + e A = C = D = 120°		b = c, d = e B = D = 90°		a = b, d = e A = 60°, D = 120°	a = b = c, d = e A = 60°, B = 120°, C = 90° D = 120°, E = 150°

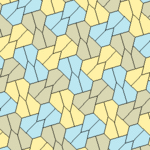
Kershner's Types (1968)

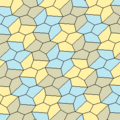
In 1968, a mathematician named Kershner found three more types of pentagons that could tile a surface. This brought the total to eight types. He thought he had found all of them, but he was wrong!

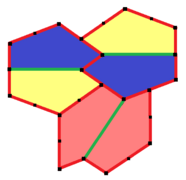
These new types (6, 7, and 8) create tilings where two different types of tile positions exist. They also tile "edge-to-edge," meaning the edges of the tiles always line up perfectly. Types 7 and 8 have chiral tiles, shown in yellow-green and blue shades.

Type 6	Type 6 (Also type 5)	Type 7	Type 8
p2 (2222)		pgg (22×)	pgg (22×)
p2 (2222)		p2 (2222)	p2 (2222)


a = d = e, b = c B + D = 180°, 2B = E	a = d = e, b = c, B = 60° A = C = D = E = 120°	b = c = d = e B + 2E = 2C + D = 360°	b = c = d = e 2B + C = D + 2E = 360°
4-tile primitive unit	4-tile primitive unit	8-tile primitive unit	8-tile primitive unit

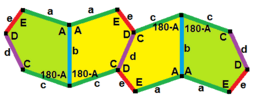
James's Type (1975)

In 1975, a person named Richard E. James III discovered a ninth type of tiling pentagon, which is now called type 10. He found it after reading about Kershner's work in a magazine. This tiling uses three different types of tile positions and is not edge-to-edge.

Type 10
p2 (2222)	cmm (2*22)


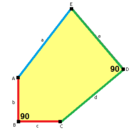
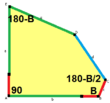a=b=c+e A=90, B+E=180° B+2C=360°	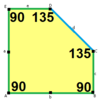a=b=2c=2e A=B=E=90° C=D=135°
6-tile primitive unit

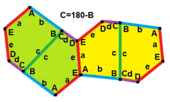
Rice's Types (1977)

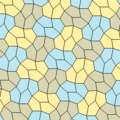
Marjorie Rice, who was not a professional mathematician, found four new types of tiling pentagons in 1976 and 1977. These are types 9, 11, 12, and 13.

All four of these tilings use two different types of tile positions. Like some earlier types, they have chiral tiles, shown in yellow-green and blue shades.

Type 9 tiles edge-to-edge, but the others do not. Each repeating unit for these tilings uses eight tiles.

Type 9	Type 11	Type 12	Type 13
pgg (22×)
p2 (2222)


b=c=d=e 2A+C=D+2E=360°	2a+c=d=e A=90°, 2B+C=360° C+E=180°	2a=d=c+e A=90°, 2B+C=360° C+E=180°	d=2a=2e B=E=90°, 2A+D=360°
8-tile primitive unit	8-tile primitive unit	8-tile primitive unit	8-tile primitive unit

Stein's Type (1985)

In 1985, Rolf Stein discovered the 14th type of pentagon that can tile a surface.

This tiling uses three different types of tile positions and is not edge-to-edge. The exact shape of this pentagon is fixed, meaning it has no "degrees of freedom" to change its angles or side lengths. The repeating unit for this tiling uses six tiles.

Type 14
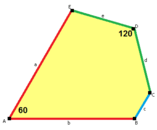
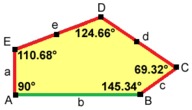	2a=2c=d=e A=90°, B≈145.34°, C≈69.32°, D≈124.66°, E≈110.68° (2B+C=360°, C+E=180°).	6-tile primitive unit

The 15th Type (2015)

In 2015, mathematicians Casey Mann, Jennifer McLoud-Mann, and David Von Derau from the University of Washington Bothell found the 15th type of pentagon that can tile a flat surface. They used a computer program to help them find it.

This tiling also uses three different types of tile positions and is not edge-to-edge. It has chiral pairs of tiles, shown with six different colors (two shades of three colors). Like Type 14, its shape is fixed. The repeating unit for this tiling uses twelve tiles.

In 2017, Michaël Rao finished his computer-assisted proof. This proof showed that these 15 pentagons are indeed the complete list of convex pentagons that can tile a flat surface. This means no other shapes of convex pentagons can tile the plane.

Type 15
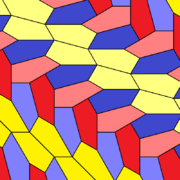(Larger image)	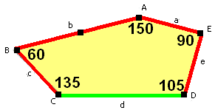a=c=e, b=2a, d= $a \sqrt 2 / \sqrt 3 -1$ A=150°, B=60°, C=135° D=105°, E=90°	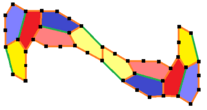12-tile primitive unit

Non-Repeating Pentagonal Tilings

Sometimes, pentagons can tile a surface in a way that doesn't repeat in a regular pattern. This is called a "nonperiodic" tiling. For example, Michael Hirschhorn created a tiling with 6-fold rotational symmetry using a pentagon with specific angles.

It has been shown that pentagons can create tilings with any number of rotational symmetries greater than two.

A pentagonal tiling with 5-fold rotational symmetry.	Hirschhorn's pentagonal tiling with 6-fold rotational symmetry.	A pentagonal tiling with 7-fold rotational symmetry.

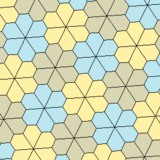
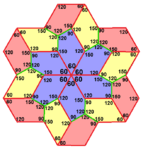
Pentagons and Hexagons

How pentagons can divide a hexagon.

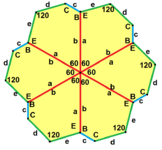
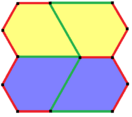
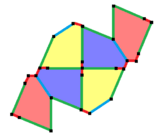
Pentagons and hexagons (six-sided shapes) have an interesting connection. Some types of hexagons can be divided into smaller pentagons. For example, a regular hexagon can be cut into two Type 1 pentagons. Other hexagons can be divided into three (Type 3), four (Type 4), or even nine (Type 3) pentagons.

Because of this, you can sometimes tile a surface with a single pentagon shape, and the way they fit together will create a pattern of hexagons.

A tiling made of Type 1 pentagons, showing how they form hexagons (each made of 2 pentagons).	A tiling made of Type 3 pentagons, showing how they form hexagons (each made of 3 pentagons).	A tiling made of Type 4 pentagons, showing how they form hexagons (each made of 4 pentagons).	A tiling made of Type 3 pentagons, showing how they form hexagons of two different sizes (made of 3 and 9 pentagons).

Non-Convex Pentagons

A repeating pattern made by the sphinx pentagon.

If a pentagon doesn't have to be "convex" (meaning all its internal angles are less than 180 degrees, so it doesn't have any "dents"), then even more types of tilings are possible.

One example is the sphinx tiling. This is a special pentagon that can be copied and scaled down to make smaller versions of itself. It can tile a surface in a non-repeating pattern, but it can also tile in a regular, repeating way.

You can also divide other shapes, like equilateral triangles, squares, or regular hexagons, into non-convex pentagons. Then, you can use these new pentagon units to tile a surface.

Pentagonal Tilings in Different Geometries

While regular pentagons can't tile a flat surface, they can tile curved surfaces:

A dodecahedron is a 3D shape with 12 regular pentagon faces. You can think of it as a tiling of 12 pentagons on the surface of a sphere. At each corner (vertex), three pentagons meet.

In hyperbolic geometry, which is a different kind of curved space, you can also have tilings made of regular pentagons. For example, the order-4 pentagonal tiling has four pentagons meeting at each corner. You can even have tilings where five, six, seven, or more pentagons meet at each corner.