Tangent space facts for kids
A tangent space in mathematics is like a flat surface or line that just touches a curved object at one specific point. Imagine a tangent line touching a circle, or a tangent plane touching a sphere. Tangent spaces help us understand how curved shapes behave in higher dimensions.
In physics, if you have something moving on a curved surface, the tangent space at any point shows all the possible directions and speeds it could be moving at that exact spot. It's like a map of all the possible "velocities" for a particle on the surface.
Contents
What is a Tangent Space?

In differential geometry, which studies shapes and spaces, we can imagine a special flat space attached to every point on a differentiable manifold. This flat space is called a tangent space. It helps us see all the directions you could move if you were just touching the curved surface at that point.
The things inside a tangent space are called tangent vectors. Think of them as arrows that start at the point and point in a direction that follows the curve. This idea is similar to how we use vectors in regular flat space.
The size, or dimension, of the tangent space is always the same as the dimension of the curved shape itself. For example, if you have a 2D surface, its tangent space at any point will be a 2D flat plane.
Tangent Space on a Sphere
Let's imagine a sphere, like a basketball. If you pick a point on the sphere, the tangent space at that point is like a flat plane that just touches the sphere there. This plane is perfectly flat and is at a right angle to the sphere's radius at that point.
If you think of a curved shape as being "inside" a bigger, flat space (like a sphere inside 3D space), then you can easily picture these tangent spaces. This old way of thinking helped scientists understand how to move things along curved paths.
Tangent Space in Algebraic Geometry
In another area of math called algebraic geometry, there's a different way to define a tangent space. This definition helps us find "smooth" points on a shape. If a shape crosses itself, like a figure-eight, it doesn't have a clear tangent line at the crossing point. These "non-smooth" points are called singular points.
Vector Fields and Movement
Once we understand tangent spaces, we can talk about vector fields. A vector field is like a map that puts a tangent vector (an arrow showing direction and speed) at every point on a curved shape.
These vector fields help us describe how things move on a curved surface. For example, if you have a particle moving on a sphere, a vector field can show its velocity at every point. This is similar to how we use ordinary differential equations to describe movement in flat space.
All the tangent spaces of a curved shape can be "glued together" to form a new, larger shape called the tangent bundle. This new shape has twice the dimension of the original one.
How Do We Define Tangent Spaces?
The simple way to describe a tangent space is to imagine the curved shape sitting inside a bigger, flat space. But mathematicians also have ways to define tangent spaces using only the curved shape itself, without needing a bigger space around it.
While thinking of tangent spaces as "velocities of curves" is easy to understand, it can be tricky to work with in complex math. More advanced methods are often used.
Definition Using Curves
Imagine a curved path passing through a point on a shape. A tangent vector at that point can be thought of as the "velocity" of that path at that exact moment.
We can group together all the paths that pass through the point and have the same "velocity" or direction at that point. Each group is called a tangent vector. The collection of all these tangent vectors at a point forms the tangent space at that point. This space doesn't change no matter how you choose to describe the curved shape.
To make the tangent space a proper vector space (where you can add vectors and multiply them by numbers), we use a special map that connects it to regular flat space. This map helps us transfer the rules of vector addition and multiplication to the tangent space.
Definition Using Derivations
Another way to define a tangent space is by using "derivations." A derivation is a special kind of rule that acts on smooth functions (functions that are very "nice" and don't have sharp corners or breaks).
This rule follows a pattern similar to the product rule in calculus. The set of all these derivations at a point forms the tangent space. This method is more abstract but very powerful in advanced mathematics.
Definition Using Cotangent Spaces
This is the most abstract way to define a tangent space. It involves looking at special groups of functions that become zero at the point we are interested in. These groups help us define something called the cotangent space. The tangent space is then defined as the "dual" of this cotangent space.
Even though this definition is complex, it's very useful because it can be applied to many different kinds of mathematical shapes, including those in algebraic geometry.
Key Features of Tangent Spaces
If a curved shape is just a flat piece of regular space (like an open part of 3D space), then its tangent spaces are simply that same flat space.
Tangent Vectors as Directional Derivatives
You can also think of tangent vectors as "directional derivatives." If you have a tangent vector, it tells you how a function changes if you move along that specific direction on the curved shape. It's like finding the slope of a hill if you walk in a certain direction.
Basis of the Tangent Space
For any smooth curved shape, we can find a set of basic tangent vectors that can be combined to make any other tangent vector at a specific point. These basic vectors form a "basis" for the tangent space, similar to how the x, y, and z axes form a basis for 3D space.
The Derivative of a Map
When you have a smooth "map" or function that transforms one curved shape into another, this map also creates a natural connection between their tangent spaces. This connection is called the "derivative," "total derivative," or "pushforward" of the map.
This derivative map tells you how the directions and speeds on the first shape are transformed into directions and speeds on the second shape. It's like a linear approximation of how the map behaves very close to a specific point.
A very important idea is that if a map smoothly transforms a small part of one shape into a small part of another, then its derivative map will smoothly transform the tangent spaces as well. This is a generalization of the inverse function theorem, which is a key idea in calculus.
See also
 In Spanish: Espacio tangente para niños
In Spanish: Espacio tangente para niños
- Coordinate-induced basis
- Cotangent space
- Differential geometry of curves
- Exponential map
- Vector space


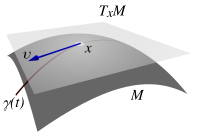
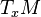 and a tangent vector
and a tangent vector 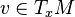 , along a curve traveling through
, along a curve traveling through 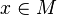 .
.