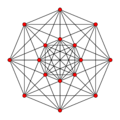
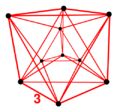
5-demicube facts for kids

In five-dimensional geometry, a demipenteract is a special type of 3D shape, but in five dimensions! Think of it as a 5-hypercube (a cube in five dimensions) where some of its corners have been removed in a specific way. This makes it a semiregular shape, meaning its faces are regular shapes, but not all of them are the same.

What is a Demipenteract?

A demipenteract is a fascinating geometric object. It's also called a 5-demicube. Imagine a regular cube, but instead of just length, width, and height, it also has two more dimensions! When you "demi" (which means "half") a hypercube, you remove half of its vertices (corners) in a special pattern. This creates a new, unique shape.

How Many Parts Does It Have?

Even though it's hard to picture, we can still count its parts:

• It has 16 vertices (corners).
• It has 80 edges (lines connecting the corners).
• It has 160 faces (flat surfaces), all of which are triangles.
• It has 120 cells (3D shapes that make up the 5D object). These cells are either tetrahedrons (pyramid-like shapes with four triangle faces).
• It has 26 "4-faces" (4D shapes that make up the 5D object). These are either 16-cells or pentachorons (which are 4D pyramids).

Who Discovered It?

The demipenteract was first described by a mathematician named Thorold Gosset. He was one of the first to study these complex shapes. He called it a "5-ic semi-regular" because it was the only semiregular 5-polytope (a 5D shape with regular but different types of faces) known at the time.

Later, in 1912, another mathematician, Emanuel Lodewijk Elte, also identified it. He gave it the name HM₅, which stood for a 5-dimensional "half measure" polytope. This name refers to how it's made by "halving" a regular hypercube.

Coxeter, a very famous geometer, later gave it the name 1₂₁. This name comes from a special diagram he used to classify these shapes, called a Coxeter diagram.

Demipenteract in the Family of Shapes

The demipenteract belongs to a special group of shapes called the "k₂₁ polytope family." It's the simplest one in this family, known as 1₂₁. Other, more complex shapes in this family include 2₂₁, 3₂₁, and 4₂₁. These shapes are all related to each other through their unique geometric properties.

What is a Petrie Polygon?

A Petrie polygon is like a special outline of a shape. Imagine looking at a 3D shape and seeing a path that goes along its edges without turning sharply. For the demipenteract, its Petrie polygon is an octagon, which is an eight-sided shape. This helps mathematicians understand its structure.

Images for kids

• 

  A projection of the demipenteract, showing its complex structure.

• 

  The vertex figure of a demipenteract, which is a rectified 5-cell.