Infinity Facts for Kids

The infinity symbol, a symbol for something that never ends.

Infinity is a super interesting idea about things that never end. You might see it written as a special symbol: 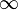$\infty$ . The word "infinity" comes from a Latin word that means "without end." Think about things that go on forever, like space or numbers – we say they are 'infinite' because they just keep going and going!

Infinity isn't like a regular number you count with, but we sometimes use it that way. It often describes how many of something there are, rather than how big something is. For example, there are infinitely many whole numbers (like 1, 2, 3, and so on), but there isn't one whole number that is infinitely big. Different types of math use infinity in slightly different ways, so its meaning can change.

There are two main ways to think about infinity:

Potential infinity: This is like a process that never stops. Imagine always adding 10 to a number. No matter how many times you add 10, you can always add 10 more! It's a never-ending process.
Actual infinity: This is a more abstract idea. For example, we know there are infinitely many numbers, even though we could never write them all down. It's a completed "set" of endless things.

Infinity in Math: Different Kinds
Math Rules for Infinity
- Adding and Multiplying with Infinity
- Dividing by Infinity
Related pages
Images for kids
See also

Infinity in Math: Different Kinds

Mathematicians have discovered that there are actually different "sizes" and "types" of infinity! It's not just one big endless thing.

Counting Endless Things

When we count things, starting with 0, 1, 2, 3, and so on, we can also talk about infinite cardinal numbers. These numbers tell us "how many" items are in a set, even if the set is endless.

One way to think about infinity is that it's a number so huge that a part of it can be the same size as the whole thing! Another way is that infinity is bigger than all the natural numbers (1, 2, 3...).

The smallest kind of infinity for counting is called countable infinity. This is the counting number for all the whole numbers and all the fractions. It has a special math symbol: 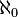$\aleph_0$ . You say it "aleph null."

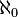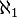It might surprise you, but there are even bigger infinite numbers! For example, the number of real numbers (which include all numbers with decimals, like 3.14159...) is larger than the number of fractions. This means there are real numbers that can't be written as fractions. The smallest infinite number bigger than $\aleph_0$ is $\aleph_1$ .

The number of mathematical functions (rules that describe how one number relates to another) is the next infinite counting number, 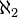$\aleph_2$ . And these numbers keep going on forever!

Ordering Endless Things

Another type of infinity deals with ordinal numbers, which describe order: "first, second, third,..." and so on.

The order "first, second, third,..." going on forever is different from an order that ends with "...third, second, first." This difference is important in advanced math. The simple "first, second, third,..." order has the math name: 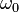$\omega_0$ (or just 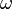$\omega$ ), which is the Greek letter omega.

Infinity on Number Lines

The third type of infinity uses the symbol 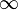$\infty$ . This symbol is often added to the real numbers (the number line) or the complex numbers.

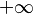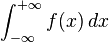You might see this symbol when a math problem involves division by zero, or when a series of numbers keeps growing (or shrinking) without any limit. For example, the series 1, 2, 3,... keeps getting bigger without any upper limit. We write this as: the limit is $+\infty$ . In calculus, a math topic, if you need to add up values over all real numbers, you might see it written like this: $\int_{-\infty}^{+\infty} f(x)\,dx$ .

Math Rules for Infinity

Each kind of infinity has its own special rules for how it works with addition, multiplication, and other operations. It's not like regular numbers!

Adding and Multiplying with Infinity

When you add or multiply with the "aleph" type of infinity (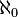 $\aleph_0$ ):

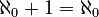Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \aleph_0 + 1 = \aleph_0 (Adding 1 to countable infinity still gives you countable infinity!)
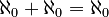Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \aleph_0 + \aleph_0 = \aleph_0 (Even two countable infinities added together is still countable infinity!)
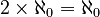Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2 \times \aleph_0 = \aleph_0 (Multiplying by 2 doesn't make it bigger!)

When you add or multiply with the "omega" type of infinity (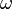 $\omega$ ):

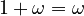
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 + \omega = \omega
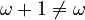Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \omega + 1 \neq \omega (This is interesting! The order matters here, unlike with regular numbers.)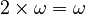
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2 \times \omega = \omega
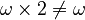Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \omega \times 2 \neq \omega (Again, order matters!)

When you use the 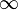$\infty$ symbol:

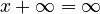Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x + \infty = \infty (Any number plus infinity is still infinity.)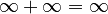
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \infty + \infty = \infty
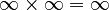
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \infty \times \infty = \infty

Dividing by Infinity

One common rule is:

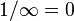$1 / \infty = 0$ (If you divide 1 by something endlessly huge, the answer gets closer and closer to zero.)

Otherwise, dividing or subtracting with infinity usually doesn't have a simple, meaningful answer in the same way regular numbers do.

Images for kids

This image shows how an infinite set can have the same number of items as a part of itself.

Infinity facts for kids

Contents