Cardinal number facts for kids
Cardinal numbers are special numbers that tell you how many of something there are. Think of them as "counting numbers." For example, when you say "I have three apples" or "There are five birds," the words "three" and "five" are cardinal numbers. They help us count objects and find out the total amount.
Contents
What are Cardinal Numbers?
Cardinal numbers answer the question "How many?" They are the numbers we use every day to count things.
- One dog
- Two friends
- Ten fingers
- One hundred stars
These numbers help us understand the size of a group of items. They are different from ordinal numbers, which tell us the order of things (like first, second, third).
Counting Big Groups: Infinity
Sometimes, we deal with groups of things that never end. These are called infinite groups. Believe it or not, mathematicians have discovered that there can be different "sizes" of infinity!
Georg Cantor and Infinite Numbers
A famous mathematician named Georg Cantor was one of the first to study these different sizes of infinity. He gave special names to these infinite cardinal numbers.
The smallest kind of infinity he found is called 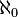 (pronounced "Aleph-null" or "Aleph-zero"). This is the number of items in a group that goes on forever, like the counting numbers: 0, 1, 2, 3, 4, and so on. Even if you count all the natural numbers (1, 2, 3, ...) or all the rational numbers (fractions like 1/2, 3/4), they all have the size of
(pronounced "Aleph-null" or "Aleph-zero"). This is the number of items in a group that goes on forever, like the counting numbers: 0, 1, 2, 3, 4, and so on. Even if you count all the natural numbers (1, 2, 3, ...) or all the rational numbers (fractions like 1/2, 3/4), they all have the size of 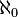 . This means you could, in theory, count them all, even though it would take forever!
. This means you could, in theory, count them all, even though it would take forever!
Even Bigger Infinities
Cantor also showed that some infinite groups are even bigger than 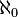 . For example, the group of real numbers is much larger. Real numbers include all the counting numbers, fractions, and also numbers with decimals that go on forever without repeating, like Pi (π).
. For example, the group of real numbers is much larger. Real numbers include all the counting numbers, fractions, and also numbers with decimals that go on forever without repeating, like Pi (π).
Cantor proved that you cannot count all the real numbers in the same way you can count the natural numbers. This means the infinity of real numbers is a "bigger" infinity than the infinity of natural numbers. It's a bit mind-bending, but it shows how amazing numbers can be!
Related pages
See also
 In Spanish: Número cardinal para niños
In Spanish: Número cardinal para niños

