Commutative algebra facts for kids

This page is about a branch of algebra. For algebras that are commutative, see Commutative algebra (structure).

A postcard from 1915 by Emmy Noether, a key figure in commutative algebra. It shows her discussing her work.

Commutative algebra is a part of algebra that studies special kinds of mathematical structures. It looks at commutative rings, their ideals, and modules that work with these rings. Think of it as a way to understand numbers and equations in a deeper sense.

This type of algebra is very important for other math areas like algebraic geometry (which uses algebra to study shapes) and algebraic number theory (which studies properties of numbers).

Some common examples of commutative rings include:

Polynomial rings: These are like equations with variables, such as x² + 2x + 1.
Rings of algebraic integers: This includes regular integers like 1, 2, 3, and also more complex numbers.
p-adic integers: These are special kinds of numbers used in advanced math.

Commutative algebra helps mathematicians understand the "local" properties of schemes, which are like generalized geometric spaces.

There's also noncommutative algebra, which studies rings where the order of multiplication matters (like A times B is not always B times A).

What is Commutative Algebra?
History of Commutative Algebra
Key Tools and Ideas
Examples of Commutative Rings
Commutative Algebra and Algebraic Geometry
See also

What is Commutative Algebra?

Commutative algebra mainly studies the rings that appear in algebraic number theory and algebraic geometry.

In algebraic number theory, special rings called rings of algebraic integers are often studied. These are a type of Dedekind ring, which is an important kind of commutative ring. Ideas from modular arithmetic (math with remainders) led to the concept of a valuation ring.

One big difference between commutative and noncommutative algebra is the idea of localization. This is a way to add "denominators" to a ring, similar to how you make fractions from whole numbers. This leads to local rings, which are rings that have only one "maximal ideal" (a special kind of ideal).

The set of all "prime ideals" in a commutative ring has a special structure called the Zariski topology. These ideas are widely used in algebraic geometry. They are the basic tools for understanding scheme theory, which is a way to generalize algebraic geometry.

Many ideas in commutative algebra are like reflections of geometric ideas. This includes concepts such as Krull dimension (a way to measure the "size" of a ring), primary decomposition, regular rings, and Cohen–Macaulay rings.

History of Commutative Algebra

This field of math was first known as ideal theory. It started with the work of Richard Dedekind on ideals in the late 1800s. His work built on earlier ideas from Ernst Kummer and Leopold Kronecker.

Later, David Hilbert introduced the word ring to describe these mathematical structures more generally. Hilbert used a more abstract way of thinking, moving away from older methods. Hilbert greatly influenced Emmy Noether. She re-explained many earlier results using what is now called the Noetherian condition. This condition describes when a chain of ideals must eventually stop growing.

Another important step was the work of Hilbert's student, Emanuel Lasker. He introduced primary ideals and proved an early version of the Lasker–Noether theorem.

The person most responsible for making commutative algebra a full subject was Wolfgang Krull. He introduced key ideas like localization and completion of a ring. He also defined the Krull dimension of a ring. Krull's work, especially his principal ideal theorem, is still seen as a very important foundation in commutative algebra. His ideas helped bring commutative algebra into algebraic geometry, which changed that field greatly.

Much of how commutative algebra is studied today focuses on modules. Both ideals and R-algebras are special types of R-modules. So, module theory helps us understand both ideals and how rings can be extended. This modern approach is often credited to Wolfgang Krull and Emmy Noether.

Key Tools and Ideas

Noetherian Rings

A Noetherian ring is a special type of ring named after Emmy Noether. In a Noetherian ring, any list of ideals that keeps getting bigger must eventually stop.

Imagine you have a chain of nested boxes, where each new box contains the previous one:

Box 1 is inside Box 2
Box 2 is inside Box 3
and so on...

In a Noetherian ring, this chain of "boxes" (ideals) cannot go on forever. It must eventually reach a point where no new, larger box can be added. This is called the ascending chain condition.

Noetherian rings are very important in algebra because they make the structure of ideals simpler. For example, the ring of integers (like 1, 2, 3) and polynomial rings are both Noetherian rings. Because of this, important theorems like the Lasker–Noether theorem and Hilbert's basis theorem apply to them.

Hilbert's Basis Theorem

This theorem is a powerful result in commutative algebra. It says: If a ring R is Noetherian, then the polynomial ring R[X] (which includes polynomials with coefficients from R) is also Noetherian.

This theorem has some important results:

If you have a Noetherian ring, then any polynomial ring with multiple variables (like R[X₀, X₁, ..., Xn-1]) will also be Noetherian.
Any set of points defined by polynomial equations (called an affine variety) can be described by just a few polynomials. This means you don't need an infinite number of equations to define a shape.
If you have an algebra that is "finitely generated" from a Noetherian ring, then it can be described by a finite number of equations.

Primary Decomposition

In math, an ideal Q is called primary if, whenever you multiply two elements x and y and their product is in Q, then either x is in Q, or y raised to some power is in Q.

Think of it like this for regular numbers: The primary ideals of the integers are like (4), (8), (9), (27), etc. These are ideals made from powers of prime numbers.

The Lasker–Noether theorem is like a generalization of the fundamental theorem of arithmetic (which says every number can be broken down into a unique set of prime numbers). This theorem states:

If R is a commutative Noetherian ring and I is an ideal, then I can be written as the intersection of a finite number of primary ideals. This breakdown is unique in a certain way.

This theorem is very useful for understanding the structure of ideals in Noetherian rings.

Localization

Localization is a mathematical process that lets you formally add "denominators" to a ring or a module. It creates a new ring or module made of fractions, like: $\frac{m}{s}$ Here, s is a special type of denominator from the original ring.

The most common example is how you get the set of rational numbers (fractions) from the set of integers (whole numbers). You start with integers and then allow division by any non-zero integer to create fractions.

Completion

Completion is another important process for rings and modules. It's similar to localization. Together, they are basic tools for studying commutative rings.

Think of it like this: If you have a set of numbers, you might want to "complete" it so that all possible "limits" of sequences within that set are also included. For example, the rational numbers can be "completed" to form the real numbers. Complete commutative rings often have a simpler structure, and a useful tool called Hensel's lemma can be applied to them.

Zariski Topology on Prime Ideals

The Zariski topology is a special way to define a "shape" or "space" for the set of all prime ideals of a ring. In this setup, the "closed sets" (which are like the basic building blocks of the space) are defined by ideals.

This idea comes from classical algebraic geometry, where closed sets are defined by polynomial equations. For example, the points where a polynomial equals zero form a closed set.

Alexander Grothendieck expanded this idea by looking at all prime ideals, not just maximal ones. This made the concept of a "scheme" possible, which is a more general way to think about geometric spaces using algebra.

Examples of Commutative Rings

The most basic example in commutative algebra is the ring of integers, written as 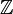$\mathbb{Z}$ . The fact that integers have prime numbers and a unique way to factor numbers into primes helped create ideas like Noetherian rings and primary decomposition.

Other important examples include:

Polynomial rings, like $R[x_1,...,x_n]$ (equations with variables).
The p-adic integers (special numbers used in advanced math).
Rings of algebraic integers (numbers that are roots of certain polynomial equations).

Commutative Algebra and Algebraic Geometry

Commutative algebra has always been a key part of algebraic geometry. Algebraic geometry uses algebraic equations to study geometric shapes.

In the late 1950s, Alexander Grothendieck introduced the idea of a scheme. This was a big step forward, generalizing the idea of algebraic varieties (shapes defined by polynomials). Schemes are built from "affine schemes," which are like local pieces. These local pieces are directly related to commutative rings. This means that studying commutative rings helps us understand these generalized geometric spaces.

The way these pieces are "glued" together uses the Zariski topology. Grothendieck also introduced more advanced "Grothendieck topologies" like the étale topology, which give a finer way to understand these spaces.