Convex regular 4-polytope facts for kids
In mathematics, a convex regular 4-polytope is a special kind of shape that exists in four dimensions. Think of them as the 4D versions of the Platonic solids (like cubes and pyramids in 3D) and regular polygons (like squares and triangles in 2D).
A Swiss mathematician named Ludwig Schläfli first described these amazing shapes in the mid-1800s. He found that there are exactly six of them. Five of these are like the 4D versions of the Platonic solids. But there's one extra shape, called the 24-cell, which doesn't have a simple 3D match.
Each of these 4D shapes is made up of 3D cells. These cells are all Platonic solids (like cubes or tetrahedra) and they fit together perfectly to form the 4D shape.
Meet the 4D Shapes!
This table shows some cool facts about the six convex regular 4-polytopes.
| Name | Family | Schläfli symbol |
Vertices (corners) |
Edges (lines) |
Faces (flat surfaces) |
Cells (3D parts) |
Dual Shape |
|---|---|---|---|---|---|---|---|
| Pentachoron 5-cell pentatope |
simplex | {3,3,3} | 5 | 10 | 10 triangles |
5 tetrahedra |
(self-dual) |
| Tesseract 8-cell hypercube |
hypercube | {4,3,3} | 16 | 32 | 24 squares |
8 cubes |
16-cell |
| Hexadecachoron 16-cell hyperoctahedron |
cross-polytope | {3,3,4} | 8 | 24 | 32 triangles |
16 tetrahedra |
tesseract |
| Icositetrachoron 24-cell |
{3,4,3} | 24 | 96 | 96 triangles |
24 octahedra |
(self-dual) | |
| Hecatonicosachoron 120-cell |
{5,3,3} | 600 | 1200 | 720 pentagons |
120 dodecahedra |
600-cell | |
| Hexacosichoron 600-cell |
{3,3,5} | 120 | 720 | 1200 triangles |
600 tetrahedra |
120-cell |
- Vertices are the points or corners of the shape.
- Edges are the lines connecting the vertices.
- Faces are the flat 2D surfaces (like triangles or squares) that make up the boundaries of the 3D cells.
- Cells are the 3D shapes (like cubes or tetrahedra) that form the "skin" of the 4D polytope.
- A Dual Shape is another shape that is related to the first one. For example, the tesseract and the 16-cell are duals of each other. Some shapes, like the 5-cell and 24-cell, are "self-dual," meaning they are their own duals!
Seeing 4D Shapes
It's hard to imagine a 4D shape, but we can try to visualize them by projecting them into 2D, just like a shadow. The tables below show different ways to look at these amazing shapes. The "Schläfli symbol" is a special code that describes each shape.
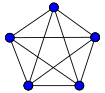
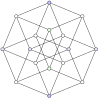
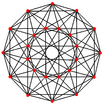
| 5-cell | 8-cell | 16-cell | 24-cell | 120-cell | 600-cell |
|---|---|---|---|---|---|
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |
   |
 |
|
|
 |
|
| These are "wireframe" pictures, like seeing the skeleton of the shape. | |||||
 |
 |
 |
 |
 |
 |
| These are "solid" pictures, showing what the shapes might look like if they were filled in. | |||||
 A tetrahedral shape |
 A cubic shape |
 An octahedral shape |
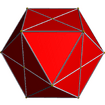 A cuboctahedral shape |
 A complex shape |
 Another complex shape |
| These are "wireframe" Schlegel diagrams, which are like seeing the shape from the inside out. | |||||
 |
 |
 |
 |
 |
 |
| These are "stereographic" projections, which show the shapes as if they were curved onto a sphere. | |||||
 |
 |
 |
 |
 |
 |
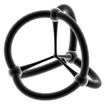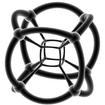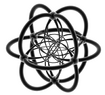Related topics
Images for kids
-
This picture shows how the different 4D shapes are related to each other.
