Discrete uniform distribution facts for kids
Probability mass function n = 5 where n = b − a + 1 |
|
Cumulative distribution function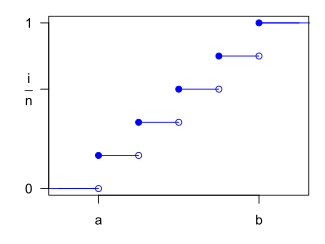 |
|
| Parameters | 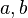 integers with integers with 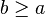  |
|---|---|
| Support | 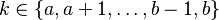 |
| Template:Probability distribution/link mass |  |
| Cumulative distribution function (cdf) | 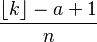 |
| Mean | 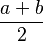 |
| Median | 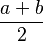 |
| Mode | N/A |
| Variance | 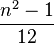 |
| Skewness | 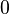 |
| Excess kurtosis | 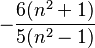 |
| Entropy | 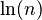 |
| Moment-generating function (mgf) | 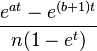 |
| Characteristic function | 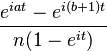 |
Imagine you have a set of things, and each one has the exact same chance of happening. That's what a discrete uniform distribution is all about! It's a way to describe situations in probability theory where every possible outcome has an equal chance.
Think about rolling a fair die. The numbers you can get are 1, 2, 3, 4, 5, or 6. Each of these numbers has an equal chance of showing up. For a fair die, the chance of rolling any specific number is 1 out of 6, or 1/6. This is a perfect example of a discrete uniform distribution.
However, if you roll two dice and add their numbers, the chances are no longer equal. For example, rolling a total of 2 (1+1) is less likely than rolling a total of 7 (like 1+6, 2+5, 3+4, etc.). So, adding two dice together does not create a uniform distribution.
While it's easy to think about this distribution with whole numbers, like the numbers on a die, it can apply to any group of items. As long as each item in the group has the same chance of being picked, it's a discrete uniform distribution.
Estimating the Maximum Number
The German Tank Problem
One interesting use of the discrete uniform distribution is trying to guess the largest possible number in a set. This is like a detective problem! It's famously known as the German tank problem.
During World War II, the Allies wanted to know how many tanks Germany was producing. They captured some German tanks and looked at their serial numbers. These serial numbers were usually given out in order, starting from 1.
If the serial numbers were like 1, 2, 3, and so on, up to a secret maximum number N, then the serial numbers on the captured tanks could be seen as a sample from a discrete uniform distribution.
By looking at the highest serial number found on a captured tank and how many tanks were captured, experts could make a good guess about the total number of tanks Germany had made. For example, if they captured 5 tanks and the highest serial number was 100, they could estimate the total production. This method was surprisingly accurate and helped the Allies understand Germany's war efforts better.
See also
 In Spanish: Distribución uniforme discreta para niños
In Spanish: Distribución uniforme discreta para niños

