Drag (physics) facts for kids
Drag is a force that slows down objects moving through a liquid or gas. Imagine pushing your hand through water; you feel a force pushing back. That's drag! When an object moves, it pushes the air or water out of its way. In return, the fluid pushes back on the object. This drag force always works in the opposite direction of the object's movement. Unlike friction between solid surfaces, drag gets stronger as an object moves faster.
Air resistance, which is another name for drag, happens when air particles hit the front of a moving object. This slows the object down. The more surface area an object has facing the direction of movement, the more air particles hit it. This means there's more resistance. For example, a big truck with a flat front has a lot of air resistance. But a sports car with a smooth, streamlined shape has much less air resistance. This allows the sports car to go faster. This is also why airplanes and other fast machines are designed to be streamlined.
Drag can also affect how fast an object falls. This is called its terminal velocity. The more drag an object has, the slower it will fall. Think about a snowflake falling. It drifts down slowly because of its shape, which creates a lot of drag. A drop of water with the same weight falls much faster because it has less drag.
Contents
History of Understanding Drag
People have known about resistance from air or other fluids for a very long time, even since the time of Aristotle. The word "drag" for this force was later used by Archibald Reith Low.
In 1922, a scientist named Louis Charles Breguet started working on ways to reduce drag by making objects more streamlined. He even designed several record-breaking aircraft in the 1920s and 1930s based on his ideas. Another important person was Ludwig Prandtl. In the 1920s, his work helped engineers understand how to reduce "skin friction," which is a type of drag.
Sir Melvill Jones also showed how important streamlining was for aircraft design. In 1929, he gave a famous presentation called 'The Streamline Airplane'. He suggested that an ideal airplane would have very little drag. This led to ideas like making planes "cleaner" (smoother) and having landing gear that could be pulled up into the plane after takeoff. Jones's ideas really surprised aircraft designers at the time. He showed how much faster planes could go with the same power if they were designed to reduce drag.
What Causes Drag?
Drag happens because of different things as an object moves through a fluid.
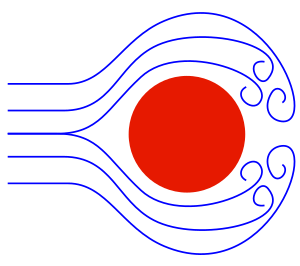
One main cause is pressure drag. As an object pushes through fluid, it creates areas of high and low pressure around it. The pressure pushing on the front of the object is usually higher than the pressure behind it. This difference in pressure creates a force that slows the object down. This is especially true for objects that aren't very streamlined.
Another cause is friction drag. This happens because the fluid sticks to the surface of the object as it moves. Imagine rubbing your hand on a rough surface; you feel friction. Similarly, the fluid creates friction as it slides along the object's surface. This friction also works to slow the object down. The smoother an object's surface, the less friction drag it will have.
When an airplane's wings create lift (the force that keeps it in the air), another type of drag appears. This is called induced drag. It's related to how the air moves around the wings to create lift.
Finally, at very high speeds, like when a jet plane flies faster than the speed of sound, wave drag can occur. This is caused by shock waves that form around the object. These shock waves create extra resistance.
In simple terms, drag can be thought of in a few ways:
- It's a mix of pressure drag and friction drag.
- It's also a mix of profile drag (from the object's shape) and induced drag (from creating lift).
- Sometimes, it's described as vortex drag, wave drag, and wake drag.
Types of Drag
| Shape and flow | Form Drag |
Skin friction |
|---|---|---|
| ≈0% | ≈100% | |
| ≈10% | ≈90% | |
 |
≈90% | ≈10% |
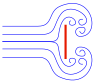 |
≈100% | ≈0% |
Here are some common types of drag:
- Form drag (or pressure drag) is caused by the size and shape of an object. A blunt, flat shape creates more form drag than a smooth, pointed shape.
- Skin friction drag (or viscous drag) comes from the friction between the fluid and the surface of the object. A rough surface will have more skin friction drag than a smooth one.
- Lift-induced drag happens when objects like wings or lifting bodies create lift. It's a side effect of generating that upward force.
- Wave drag in aerodynamics happens when an aircraft flies at very high speeds, close to or above the speed of sound. It's caused by shock waves. For example, the supersonic Concorde aircraft was designed to reduce this type of drag.
- Wave resistance (in ship design) happens when a boat moves through water and creates waves on the surface. These waves take energy away from the boat, slowing it down.
- Boat-tail drag on an aircraft is caused by how the back part of the plane or engine narrows down. If it narrows too sharply, it can create extra drag.
The Drag Equation
Scientists use an equation to figure out how much drag an object will experience. Drag depends on the fluid it's moving through, and the object's size, shape, and speed.
The main drag equation looks like this: 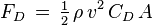 Let's break down what each part means:
Let's break down what each part means:
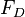 is the drag force itself. This is the force that slows the object down.
is the drag force itself. This is the force that slows the object down.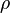 (pronounced "rho") is the density of the fluid. For example, air is less dense than water.
(pronounced "rho") is the density of the fluid. For example, air is less dense than water.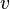 is the speed of the object as it moves through the fluid.
is the speed of the object as it moves through the fluid. is the cross-sectional area of the object. Imagine slicing the object where it's widest, facing the direction of movement. That's the area.
is the cross-sectional area of the object. Imagine slicing the object where it's widest, facing the direction of movement. That's the area.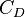 is the drag coefficient. This is a special number that shows how "slippery" or "draggy" an object's shape is. A lower drag coefficient means less drag.
is the drag coefficient. This is a special number that shows how "slippery" or "draggy" an object's shape is. A lower drag coefficient means less drag.
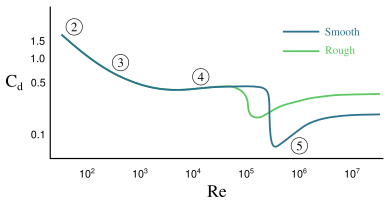
The drag coefficient (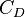 ) changes depending on the object's shape and how fast it's moving relative to the fluid.
) changes depending on the object's shape and how fast it's moving relative to the fluid.
At slower speeds, the drag force is directly related to the speed. This means if you double the speed, you double the drag. But at higher speeds, drag increases much faster. It becomes related to the square of the speed. So, if you double the speed, the drag force can become four times stronger! This is why it takes a lot more power to go very fast.
Images for kids
See also
 In Spanish: Resistencia (fluidos) para niños
In Spanish: Resistencia (fluidos) para niños
 | Roy Wilkins |
 | John Lewis |
 | Linda Carol Brown |