e (mathematical constant) facts for kids

e is a very special number in mathematics, roughly equal to 2.71828. It's known by a few names, like Euler's number (named after the Swiss mathematician Leonhard Euler) or Napier's constant (after the Scottish mathematician John Napier). This number is just as important in math as π (Pi) and i (the imaginary unit).

The number e is an irrational number. This means you can't write it as a simple fraction using two whole numbers. Its decimal goes on forever without repeating, like 2.718281828459045... The mathematician Euler himself calculated the first 23 digits of e.

e was first discovered in 1683 by the Swiss mathematician Jacob Bernoulli. He found it while studying how compound interest grows over time.

What is the Number e?

The number e is a fundamental mathematical constant, much like 0, 1, π, and i. These five numbers are incredibly important and appear often in different areas of mathematics. For example, they all come together in a famous formula called Euler's identity. Just like Pi, e is also an irrational number, meaning it can't be written as a simple fraction. It's also a transcendental number, which means it's not the solution to any basic polynomial equation with whole number coefficients.

How Was e Discovered?

The story of e began with Jacob Bernoulli in 1683. He was looking at a problem about compound interest. Imagine you put money in a bank, and it earns interest. If the interest is added to your money more and more often (like every month, every day, or even every second), how much would your money grow? Bernoulli found that as the interest was compounded more and more frequently, the total amount approached a specific number – that number was e!

e and Growth: The Exponential Function

The number e is super important for understanding exponential functions. These functions describe things that grow or shrink very quickly, like populations, radioactive decay, or even how money grows with compound interest. For example, if you have an exponential function where the base is e, it describes a very natural kind of growth. When you apply this special exponential function to the number one, the result is exactly e!

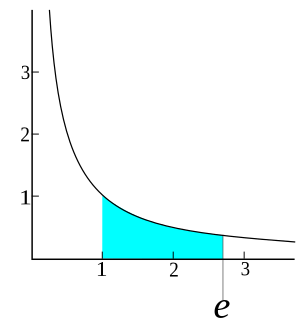
Finding e: A Limit Explained

The blue area under the curve y=1/x, from 1 to e, is exactly 1. This is another way to define e!

One way to think about e is by looking at what happens when a certain mathematical expression gets closer and closer to a specific value. Jacob Bernoulli, when he discovered e, was trying to figure out what number the expression 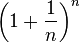approaches as 'n' gets incredibly large. As 'n' grows bigger and bigger, this expression gets closer and closer to the value of e.

Images for kids

• 

  The five colored regions are of equal area, and define units of hyperbolic angle along the {{{1}}}

See also

In Spanish: Número e para niños