Field (mathematics) facts for kids

A field in mathematics is a special kind of algebraic structure. Think of it as a set of numbers where you can do all the basic math operations: adding, subtracting, multiplying, and dividing. The only rule for division is that you can't divide by zero!

A field is like a super-powered ring because it adds the ability to divide. Good examples of fields are the rational numbers (like fractions) and the real numbers (all the numbers on a number line). Sometimes, mathematicians use the symbol 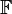to stand for a field.

What Makes a Field Special?

A field has a set of elements (let's call it R) and two main operations: addition (+) and multiplication (•). These operations must follow a set of rules. Since a field is also a ring, it follows all the rules for rings, plus a few extra ones.

Rules for Addition and Multiplication

Here are the rules that make a set a field:

Closure: Staying in the Set

When you add or multiply any two elements from the set, the answer must also be in that same set.

• If you add any two numbers 'a' and 'b' from R, the result (a + b) is also in R.
• If you multiply any two numbers 'a' and 'b' from R, the result (a • b) is also in R.

Identity Elements: Special Numbers

There are two very special numbers in a field:

• Additive Identity (Zero): There's a number, called zero (0), that doesn't change any other number when you add it.
  • For any number 'a' in R, 0 + a = a + 0 = a.
• Multiplicative Identity (One): There's another number, called one (1), that doesn't change any other number when you multiply it. This '1' must be different from '0'.
  • For any number 'a' in R, 1 • a = a • 1 = a.

Associativity: Grouping Doesn't Matter

When you add or multiply more than two numbers, it doesn't matter how you group them with parentheses; the final answer will be the same.

• For Addition: (a + b) + c = a + (b + c)
• For Multiplication: (a • b) • c = a • (b • c)

Commutativity: Order Doesn't Matter

When you add or multiply two numbers, the order in which you do it doesn't change the answer.

• For Addition: a + b = b + a
• For Multiplication: a • b = b • a

Inverse Elements: Getting Back to Identity

Every number in the set has an "opposite" that helps you get back to the identity elements.

• Additive Inverse: For every number 'a' in R, there's a number '-a' (its opposite) such that when you add them, you get zero.
  • a + (-a) = 0
• Multiplicative Inverse: For every number 'a' in R (except for zero), there's a number 'a^-1' (its reciprocal) such that when you multiply them, you get one. This is what allows division!
  • a • a^-1 = 1

Distribution: Mixing Operations

Multiplication and addition work well together in a field. This rule shows how multiplication spreads over addition.

• a • (b + c) = (a • b) + (a • c)
• (a + b) • c = (a • c) + (b • c)

Examples of Fields You Know

You use fields all the time without even realizing it!

• The set of rational numbers (): These are numbers that can be written as a fraction, like 1/2, -3/4, or 5. You can add, subtract, multiply, and divide them (except by zero).
• The set of real numbers (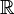): This includes all rational numbers, plus numbers like pi (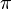) or the square root of 2.
• The set of complex numbers (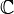): These numbers involve the imaginary unit 'i' (where i² = -1).

The set of integers (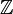) is NOT a field. Why? Because if you divide two integers, the answer isn't always an integer (e.g., 1 divided by 2 is 0.5, which isn't an integer). This breaks the "closure" rule for division.

Related pages

• Group (mathematics)

Images for kids

• 

  This shape is a compact Riemann surface. In higher math, fields of functions are used to study its properties.

• 

  The hairy ball theorem is a fun math idea! It says you can't comb all the hair flat on a ball without creating a swirl or a bald spot. This relates to how vector fields behave on spheres.

See also

In Spanish: Cuerpo (matemáticas) para niños