kids encyclopedia robot

Magnetic reluctance facts for kids

Kids Encyclopedia Facts

Magnetic reluctance, also known as magnetic resistance, is a way to measure how much a material "resists" a magnetic field. Think of it like electrical resistance in an electric circuit. But instead of using up magnetic energy, reluctance helps store it. Just as electricity follows the easiest path, a magnetic field will follow the path with the least magnetic reluctance.

We usually show magnetic reluctance with the symbol ℜ. It's a scalar quantity, meaning it only has a size, not a direction.

History of Magnetic Reluctance

The idea of magnetic resistance was first talked about by James Prescott Joule in the 1800s. The term "magnetic reluctance" was created in May 1888 by Oliver Heaviside. The term "magnetomotive force" (MMF) was first named by Bosanquet. The idea of a law for magnetic flux, similar to Ohm's law for electric circuits, is credited to Henry Augustus Rowland.

Understanding Magnetic Reluctance

Magnetic reluctance is the ratio of the "magnetomotive force" (MMF) in a magnetic circuit to the magnetic flux in that circuit. In simpler terms, it tells you how much "push" (MMF) is needed to create a certain amount of magnetic flow (magnetic flux) through a material.

We can write this as a formula: 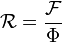\mathcal R = \frac{\mathcal F}{\Phi}

Here's what the symbols mean:

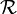  • \mathcal R (pronounced "R") is the reluctance. Its unit is ampere-turns per weber. This is the same as turns per henry.
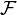  • \mathcal F (pronounced "F") is the magnetomotive force (MMF). Its unit is ampere-turns.
  • Φ (pronounced "Phi") is the magnetic flux. Its unit is webers.

This formula is sometimes called Hopkinson's law. It's a lot like Ohm's law in electricity, where:

  • Reluctance is like electrical resistance.
  • MMF is like voltage.
  • Magnetic flux is like electric current.

Magnetic flux always forms a closed loop, as described by Maxwell's equations. However, the path of this loop depends on the reluctance of the materials around it. Magnetic flux tends to concentrate in paths with the lowest reluctance.

Materials like air and a vacuum have high reluctance. Materials that are easily magnetized, such as soft iron, have low reluctance. When magnetic flux concentrates in low-reluctance materials, it creates strong temporary poles. This causes mechanical forces that pull these materials towards areas of higher flux, always resulting in an attractive force.

Calculating Reluctance

The reluctance of a uniform magnetic circuit can be calculated using this formula: 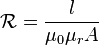\mathcal R = \frac{l}{\mu_0 \mu_r A} Or, more simply: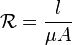 \mathcal R = \frac{l}{\mu A}

Let's break down these parts:

  • l is the length of the magnetic circuit in metres.
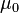  • \mu_0 is the permeability of free space. This is a constant value, 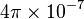4 \pi \times 10^{-7} henry per metre.
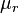  • \mu_r is the relative magnetic permeability of the material. This number shows how easily a material can be magnetized compared to a vacuum. It has no units.
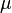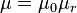  • \mu is the overall permeability of the material (where \mu = \mu_0 \mu_r ).
  • A is the cross-sectional area of the circuit in square metres.

The opposite of reluctance is called permeance. It shows how easily a material allows magnetic flux to pass through it. 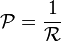\mathcal P = \frac{1}{\mathcal R} The SI unit for permeance is the henry.

Uses of Magnetic Reluctance

Magnetic reluctance is used in many different technologies:

  • Transformers: Sometimes, small air gaps are put into the cores of transformers. This increases the reluctance of the magnetic circuit. It helps the transformer store more energy before its core becomes "saturated" (meaning it can't hold any more magnetic field). This is also used in flyback transformers.
  • Reluctance Motors: The way reluctance motors work is based on changing reluctance. These motors are designed so that their moving parts are pulled towards the position where the magnetic circuit has the lowest reluctance. This creates a turning force.
  • Magnetic Shielding: Loudspeakers often have magnetic shielding. This is usually a cover made of a material like soft iron around the speaker magnet. This material has low reluctance, so it helps to contain the speaker's magnetic field. This stops the speaker from interfering with other electronics, like old CRT televisions.

Reluctance is also important in:

  • Variable reluctance (magnetic) pickups used in some musical instruments.

Related pages

  • Dielectric complex reluctance
  • Magnetic capacitivity
  • Magnetic capacitance
  • Magnetic circuit
  • Magnetic complex reluctance
  • Reluctance motor

See also

Kids robot.svg In Spanish: Reluctancia magnética para niños

kids search engine
All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Magnetic reluctance Facts for Kids. Kiddle Encyclopedia.