Roger Apéry facts for kids
Quick facts for kids
Roger Apéry
|
|
|---|---|
| Born | 14 November 1916 |
| Died | 18 December 1994 (aged 78) |
| Nationality | French |
| Education | Lycée Louis-le-Grand |
| Alma mater | École normale supérieure |
| Occupation | Mathematician |
Roger Apéry (born November 14, 1916, in Rouen, France – died December 18, 1994, in Caen, France) was a French mathematician. He is best known for something called Apéry's theorem. This theorem states that a special number, written as ζ(3), is an irrational number. An irrational number is a number that cannot be written as a simple fraction (like 1/2 or 3/4). The symbol ζ(s) stands for a math function called the Riemann zeta function.
Contents
About Roger Apéry
Roger Apéry was born in Rouen in 1916. His mother was French and his father was Greek. He spent his early years in Lille before his family moved to Paris in 1926. There, he went to high school at Lycée Ledru-Rollin and Lycée Louis-le-Grand.
In 1935, he was accepted into a very famous French school called the École normale supérieure. His studies were put on hold when World War II began. He joined the army in 1939 and was captured in 1940. He was released in 1941 due to illness.
After the war, he finished his advanced studies. In 1947, he earned his doctorate degree (a very high academic degree) in a field of math called algebraic geometry. This area of math uses algebra to study shapes and spaces.
His Work as a Professor
In 1947, Apéry became a lecturer (a type of university teacher) at the University of Rennes. Two years later, in 1949, he became a Professor at the University of Caen. He taught and researched there until he retired.
Apéry's Famous Theorem
In 1979, Roger Apéry surprised the math world with a proof. He showed that the number ζ(3) is irrational. This number is found by adding up a special series: 1/1³ + 1/2³ + 1/3³ + 1/4³ + ... and so on forever.
This was a very difficult problem to solve. Mathematicians still don't know if similar numbers (like 1/1⁵ + 1/2⁵ + 1/3⁵ + ...) are irrational or not. Because of Apéry's breakthrough, many other mathematicians have worked on "Apéry sequences." They hope to find new ways to prove if other similar numbers are irrational.
His Political Interests
Roger Apéry was also interested in politics. For a few years in the 1960s, he was the president of a political group in the Calvados area called the Radical Party of the Left. He stopped being active in politics after some big changes happened in universities in 1968. He felt that university life was changing in ways he didn't agree with.
His Family and Later Life
Roger Apéry got married in 1947 and had three sons. One of his sons, François Apéry, also became a mathematician. His first marriage ended in 1971, and he remarried in 1972, but that marriage also ended in 1977.
In 1994, Roger Apéry passed away in Caen after a long illness called Parkinson's disease, which affects movement. He was buried in Père Lachaise Cemetery in Paris, next to his parents. His tombstone has a special math message on it, showing his famous theorem: 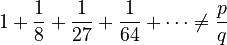 This math means that the sum of the inverses of cubes (like 1/1³, 1/2³, 1/3³...) is not equal to a simple fraction (p/q). This is another way of saying it's an irrational number.
This math means that the sum of the inverses of cubes (like 1/1³, 1/2³, 1/3³...) is not equal to a simple fraction (p/q). This is another way of saying it's an irrational number.
See also
- Apéry's constant
- Basel problem

