4-polytope facts for kids

Kids Encyclopedia Facts

Cool 4D Shapes: The Six Regular 4-Polytopes
{3,3,3}	{3,3,4}	{4,3,3}
The 5-cell Also called Pentatope	The 16-cell Also called Orthoplex	The 8-cell Also called Tesseract
{3,4,3}	{3,3,5}	{5,3,3}
The 24-cell Also called Octaplex	The 600-cell Also called Tetraplex	The 120-cell Also called Dodecaplex

In geometry, a 4-polytope is a special shape that exists in four dimensions. Think of it as the 4D version of a polygon (like a square in 2D) or a polyhedron (like a cube in 3D). These amazing shapes are also sometimes called polychorons or polycells.

A 4-polytope is a closed figure, meaning it has a clear inside and outside. It's made up of different parts:

Vertices: These are the corner points.
Edges: These are the lines connecting the vertices.
Faces: These are flat shapes like polygons (squares, triangles, etc.).
Cells: These are 3D shapes like polyhedra (cubes, pyramids, etc.).

Every face in a 4-polytope is shared by exactly two cells. This is similar to how each edge of a 3D polyhedron connects exactly two faces. The first person to discover these fascinating 4D shapes was a Swiss mathematician named Ludwig Schläfli, before 1853.

What is a 4-Polytope?
- Parts of a 4-Polytope
Exploring 4-Polytope Geometry
- The Six Regular 4-Polytopes
How Do We See 4-Polytopes?
Understanding 4-Polytope Types
- Key Features for Classification
- Main Categories of 4-Polytopes
Images for kids
See Also

What is a 4-Polytope?

A 4-polytope is a complete shape in four dimensions. It's built from smaller parts. Imagine a 3D cube is made of 2D squares (faces). A 4D shape is made of 3D shapes (cells).

Parts of a 4-Polytope

Vertices are the points where edges meet.
Edges are the lines connecting vertices.
Faces are the flat polygon shapes.
Cells are the 3D polyhedra that make up the "skin" of the 4-polytope.

Each face of a 4-polytope connects exactly two cells. This is like how each edge of a cube connects two of its square faces. Also, a 4-polytope cannot be split into two or more smaller 4-polytopes.

Exploring 4-Polytope Geometry

The most famous 4-polytope is the tesseract, also known as the hypercube. It's the 4D version of a simple 3D cube. Just like there are special 3D shapes called Platonic solids (like the cube or pyramid), there are also special 4D shapes called convex regular 4-polytopes.

The Six Regular 4-Polytopes

There are six main types of these regular 4-polytopes. They are like the "perfect" shapes in four dimensions.

The 5-cell (like a 4D pyramid)
The 8-cell (the tesseract or hypercube)
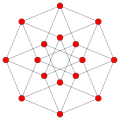
The 16-cell (like a 4D diamond)
The 24-cell
The 120-cell
The 600-cell

These shapes can be ordered by their "size" or "hypervolume" if they all have the same radius. The 5-cell is the smallest, and the 120-cell is the largest. As you go from the 5-cell to the 120-cell, the shapes become "rounder" and more complex.

Regular convex 4-polytopes
Symmetry group	A₄	B₄		F₄	H₄
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2	𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2	𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2
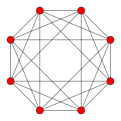
Graph
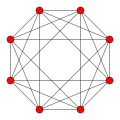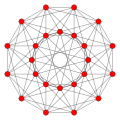Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical	120 icosahedral	600 tetrahedral
Edges	10 triangular	24 square	32 triangular	96 triangular	720 pentagonal	1200 triangular
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	675 in 120-cell	2 16-cells	3 8-cells	25 24-cells	10 600-cells
Great polygons		2 squares x 3	4 rectangles x 4	4 hexagons x 4	12 decagons x 6	100 irregular hexagons x 4
Petrie polygons	1 pentagon	1 octagon	2 octagons	2 dodecagons	4 30-gons	20 30-gons
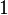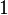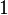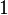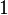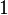Long radius	$1$	$1$	$1$	$1$	$1$	$1$
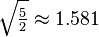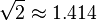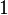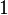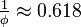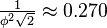Edge length	$\sqrt{\tfrac{5}{2}} \approx 1.581$	$\sqrt{2} \approx 1.414$	$1$	$1$	$\tfrac{1}{\phi} \approx 0.618$	$\tfrac{1}{\phi^2\sqrt{2}} \approx 0.270$
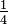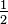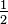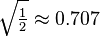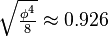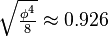Short radius	$\tfrac{1}{4}$	$\tfrac{1}{2}$	$\tfrac{1}{2}$	$\sqrt{\tfrac{1}{2}} \approx 0.707$	$\sqrt{\tfrac{\phi^4}{8}} \approx 0.926$	$\sqrt{\tfrac{\phi^4}{8}} \approx 0.926$
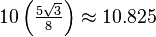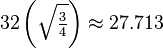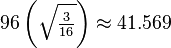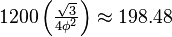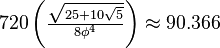Area	$10\left(\tfrac{5\sqrt{3}}{8}\right) \approx 10.825$	$32\left(\sqrt{\tfrac{3}{4}}\right) \approx 27.713$	$24$	$96\left(\sqrt{\tfrac{3}{16}}\right) \approx 41.569$	$1200\left(\tfrac{\sqrt{3}}{4\phi^2}\right) \approx 198.48$	$720\left(\tfrac{\sqrt{25+10\sqrt{5}}}{8\phi^4}\right) \approx 90.366$
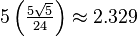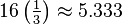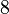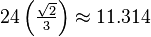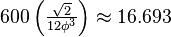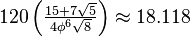Volume	$5\left(\tfrac{5\sqrt{5}}{24}\right) \approx 2.329$	$16\left(\tfrac{1}{3}\right) \approx 5.333$	$8$	$24\left(\tfrac{\sqrt{2}}{3}\right) \approx 11.314$	$600\left(\tfrac{\sqrt{2}}{12\phi^3}\right) \approx 16.693$	$120\left(\tfrac{15 + 7\sqrt{5}}{4\phi^6\sqrt{8}}\right) \approx 18.118$
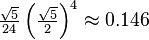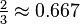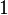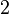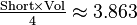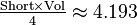4-Content	$\tfrac{\sqrt{5}}{24}\left(\tfrac{\sqrt{5}}{2}\right)^4 \approx 0.146$	$\tfrac{2}{3} \approx 0.667$	$1$	$2$	$\tfrac{\text{Short}\times\text{Vol}}{4} \approx 3.863$	$\tfrac{\text{Short}\times\text{Vol}}{4} \approx 4.193$

How Do We See 4-Polytopes?

It's impossible to see a 4-polytope directly in our 3D world. But mathematicians use clever tricks to help us imagine them.

Ways to Show a 24-cell
Slicing		Unfolding

Projections (Flattening)
Schlegel Diagram	2D Flat View	3D Flat View

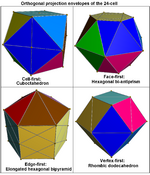Orthogonal Projection

Imagine shining a light through a 3D object onto a flat wall to see its shadow. That's a projection. For 4-polytopes, we can project them onto 2D or 3D space.

A 2D projection might look like a drawing of lines and points.
A 3D projection can show the outer "shell" of the shape.

Perspective Projection

This is like taking a photo. A Schlegel diagram is a common way to do this. It projects the 4-polytope onto a 3D space. It shows the vertices, edges, faces, and cells as if they were inside a giant sphere.

Sectioning (Slicing)

Think about slicing an orange. Each slice shows a 2D circle. If you slice a 3D polyhedron, you get a 2D shape. If you slice a 4-polytope, you get a 3D shape! By looking at many slices in a row, you can get an idea of the whole 4D shape. Sometimes, these slices are animated to show how the shape changes over "time" (the fourth dimension).

Nets (Unfolding)

A net of a 4-polytope is like unfolding it into 3D space. Imagine unfolding a cardboard box; its faces lie flat. For a 4-polytope, its 3D "cells" would be connected by their faces and lie flat in 3D space.

Understanding 4-Polytope Types

Just like we classify animals or plants, mathematicians classify 4-polytopes based on their features.

Key Features for Classification

Convexity: A 4-polytope is convex if it doesn't "bend in" or cross itself. If you pick any two points inside a convex 4-polytope, the line connecting them stays entirely inside. If it's not convex, it might be a star 4-polytope, which looks spiky.
Regularity: A 4-polytope is regular if all its parts are exactly the same. This means all its cells are identical regular polyhedra (like cubes or tetrahedrons), and all its vertices look the same.
Semi-regularity: A 4-polytope is semi-regular if all its vertices are the same, and its cells are regular polyhedra. The cells might be different types, but their faces must be the same kind of polygon.
Uniformity: A 4-polytope is uniform if all its vertices are the same, and its cells are uniform polyhedra. The faces of a uniform 4-polytope must be regular shapes.
Prismatic: A 4-polytope is prismatic if it's made by combining two or more simpler shapes. For example, the tesseract can be seen as a "product" of a cube and a line segment.
Tessellations (Honeycombs): These are infinite patterns that fill up 3D space, like a honeycomb. They are like infinite 4-polytopes. The cubic honeycomb is a famous example, where cubes fill all of 3D space without gaps.

Main Categories of 4-Polytopes

Here are some of the main groups of 4-polytopes that mathematicians study:

Uniform 4-Polytopes

These are shapes where all vertices are identical.

Convex Uniform 4-Polytopes: There are 64 of these, plus two endless families.
- The 6 regular 4-polytopes (like the tesseract) are part of this group.
- There are also prismatic types, like polyhedral hyperprisms (which include the hypercube).
Non-convex Uniform 4-Polytopes: These are the spiky or self-intersecting ones.
- There are 10 regular star 4-polytopes. The great grand stellated 120-cell is the largest of these, with 600 vertices.

Other Convex 4-Polytopes

These include shapes like:

Polyhedral pyramids (a 3D polyhedron extended into 4D)
Polyhedral bipyramids
Polyhedral prisms

Infinite 4-Polytopes (Honeycombs)

These shapes fill up space without end.

In Euclidean 3-space: There are 28 convex uniform honeycombs. The regular cubic honeycomb is one example, where cubes perfectly fill 3D space.
In Hyperbolic 3-space: There are 76 types of these honeycombs in a special kind of curved space.

Dual Uniform 4-Polytopes

For many uniform 4-polytopes, there's a "dual" shape. These duals have identical cells.

There are 41 unique dual convex uniform 4-polytopes.

Abstract Regular 4-Polytopes

These are shapes that exist more in mathematical ideas than in physical space. They don't always look like "normal" shapes.

The 11-cell
The 57-cell

These categories cover 4-polytopes with a lot of symmetry. Many other 4-polytopes exist, but they are not studied as much because they are less "perfect."

Images for kids

The tesseract as a Schlegel diagram
The truncated 120-cell is one of 47 convex non-prismatic uniform 4-polytopes
The great grand stellated 120-cell is the largest of 10 regular star 4-polytopes, having 600 vertices.
The regular cubic honeycomb is the only infinite regular 4-polytope in Euclidean 3-dimensional space.
The 11-cell is an abstract regular 4-polytope, existing in the real projective plane, it can be seen by presenting its 11 hemi-icosahedral vertices and cells by index and color.