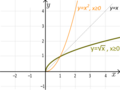Bijective function Facts for Kids


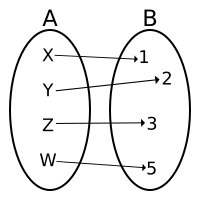Bijection. There is exactly one arrow to every element in the codomain B (from an element of the domain A).

In mathematics, a bijective function or bijection is a special kind of function. Imagine a function as a rule that connects each item from one group (called the domain) to an item in another group (called the codomain).

A function is a bijection if it meets two important conditions:

It's an injection (also called "one-to-one"): This means that every different input from the domain leads to a different output in the codomain. No two inputs go to the same output.
It's a surjection (also called "onto"): This means that every single item in the codomain is "hit" or "reached" by at least one input from the domain. There are no unused items in the codomain.

When a function is both an injection and a surjection, it's a bijection. This means that for every item in the codomain, there is exactly one item in the domain that connects to it. Think of it like a perfect pairing, where every item in the first group has a unique partner in the second group, and no one is left out. Another name for a bijection is a one-to-one correspondence.

The words bijection, surjection, and injection were first used by a group of mathematicians called Nicholas Bourbaki in the 1930s. They wrote many books about advanced mathematics.


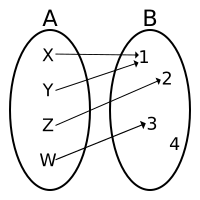Not a bijection. (It is not a surjection. It is not an injection.)

What Makes a Function a Bijection?
Bijections and Set Sizes
Bijections and Inverse Functions
Examples of Bijective Functions
Related Pages
Images for kids
See also

What Makes a Function a Bijection?

A function f that goes from a set A (the domain) to a set B (the codomain) is a bijection if:

Every item in B is the image of exactly one item in A.
Every item in B has exactly one pre-image in A.

Let's break that down:

If a function is a surjection, it means every item in B has at least one pre-image in A.
If a function is an injection, it means every item in B has at most one pre-image in A.
So, if a function is a bijection, it means every item in B has exactly one pre-image in A. It's a perfect match!

Bijections and Set Sizes

Cardinality is a fancy word for the number of elements in a set. For example, if set A has {apple, banana, cherry}, its cardinality is 3. We can write this as #A=3.

Two sets, let's say A and B, have the same cardinality if you can find a bijection between them. This means you can perfectly pair up every item in A with every item in B, with no items left over in either set. So, if #A = #B, it means there's a bijection from A to B.

Bijections and Inverse Functions

Bijections are closely connected to inverse functions. An inverse function basically "undoes" what the original function did. If a function f takes you from A to B, its inverse function g takes you back from B to A.

Think of it like this: if f(a) = b (meaning a goes to b), then the inverse function g(b) = a (meaning b goes back to a).

If you apply a function and then its inverse, you get back to where you started.
A function can only have an inverse function if it is a bijection. If it's not a bijection, you can't perfectly reverse it.

Important Note: The symbol for an inverse function can be a bit confusing. For a function f, its inverse is often written as f^-1(x). But be careful! This is different from x^-1, which means 1 divided by x (like 2^-1 = 1/2).

Examples of Bijective Functions

Let's look at some common functions and see if they are bijections. We'll often think about functions where both the input (x) and output (y) are real numbers (all numbers on the number line).

Visualizing Bijections with Graphs

When you look at the graph of a function:

Graphic meaning: A function is a bijection if every horizontal line you can draw crosses the graph in exactly one spot.

* If a horizontal line crosses more than once, it's not an injection. * If a horizontal line doesn't cross at all, it's not a surjection.

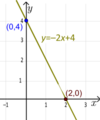
Example: A linear function like y = ax + b (where a is not zero, so it's a slanted line) is a bijection.

If you draw any horizontal line, it will cross a slanted line only once. This means it's both an injection and a surjection.

Example: The polynomial function f(x) = x³ is a bijection.

Its graph looks like a wavy line that always goes up. Any horizontal line will cross it exactly once.
Its inverse function is the cube root function, f(x) = ∛x, which is also a bijection.

Example: The quadratic function f(x) = x² is not a bijection if we consider all real numbers for input and output.

If you draw a horizontal line above the x-axis, it will cross the parabola twice (e.g., y=4 is crossed by x=2 and x=-2). So, it's not an injection.
If you draw a horizontal line below the x-axis, it won't cross the parabola at all. So, it's not a surjection (because you can't get negative outputs from x²).

Changing the Domain and Codomain

The last example shows something important: to know if a function is a bijection, you need to know three things:

The domain (what numbers you can put into the function).
The function machine (the rule itself, like x²).
The codomain (what numbers are possible outputs).

Example: Let's use the function machine f(x) = x² again.

If the domain is all real numbers (ℝ) and the codomain is all real numbers (ℝ), then f(x) = x² is not a bijection.
However, if we change the domain to only non-negative numbers ([0,+∞), meaning 0 and all positive numbers) and the codomain to only non-negative numbers ([0,+∞)), then this same machine f(x) = x² is a bijection!

* Every non-negative output comes from exactly one non-negative input.

More Examples of Bijections and Their Inverses

The square root function f(x) = √x is a bijection if its domain is [0,+∞) and its codomain is [0,+∞). It's the inverse of f(x) = x² when both are restricted to non-negative numbers.

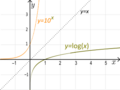
The exponential function f(x) = a^x (where a is a number greater than 1, like 10^x) is a bijection if its domain is all real numbers (ℝ) and its codomain is only positive numbers ((0,+∞)). This is because a^x can never be zero or negative.

The logarithmic function f(x) = log_ax (like log₁₀x) is a bijection if its domain is positive numbers ((0,+∞)) and its codomain is all real numbers (ℝ). It's the inverse of the exponential function a^x.

Images for kids

1. Bijection. All slanted lines are bijections f(x):ℝ→ℝ.
2. Bijection. f(x):ℝ→ℝ. f(x)=x³.
3. Not a bijection. f(x):ℝ→ℝ. f(x)=x² is not a surjection. It is not an injection.
4. Bijections. f(x):ℝ→ (0,+∞). f(x)=10^x (thin yellow) and its inverse f(x):(0,+∞)→ℝ. f(x)=log₁₀x (thick green).
5. Bijections. f(x):ℝ→ℝ. f(x)=x³ (thin yellow) and its inverse f(x)=∛x (thick green).
6. Bijections. f(x):[0,+∞)→[0,+∞). f(x)=x² (thin yellow) and its inverse f(x)=√x (thick green).