Coastline paradox facts for kids
The coastline paradox is a surprising fact in geography and mathematics. It states that a coastline does not have one specific, fixed length. Instead, the measured length depends on the ruler or scale used to measure it.
This happens because coastlines are jagged and irregular. They are not smooth straight lines. This concept is related to fractal geometry. The phenomenon was first studied by Lewis Fry Richardson and later explained by Benoit Mandelbrot.
Contents
How Was It Discovered?
Before 1951, a scientist named Lewis Fry Richardson was studying borders between countries. He noticed something strange about the border between Spain and Portugal.
- The Spanish geographers said the border was 987 km (613 mi) long.
- The Portuguese geographers said it was 1,214 km (754 mi) long.
Neither side was making a mistake. The difference came from the measuring tools they used. One group used a shorter ruler than the other. Richardson realized that using a shorter ruler allows you to measure more of the small twists and turns in the border. This makes the total length appear longer. This is now known as the "Richardson effect".
Mathematics of Rough Shapes
Smooth Curves vs. Rough Lines
In standard geometry, simple shapes like circles have a fixed perimeter. If you measure a smooth circle with smaller and smaller straight lines, you eventually get a specific number. This is called the circumference.
Coastlines are different. They are rough and bumpy at every scale. If you zoom in on a map of a coast, you see large bays. If you zoom in closer, you see smaller inlets. If you look at the ground, you see rocks and pebbles. This pattern repeats down to tiny grains of sand.
What Is a Fractal?
Benoit Mandelbrot developed a type of math called fractal geometry to explain this. He coined the term "fractal" from the Latin word for "broken" or "fractured".
A fractal is a shape that looks similar no matter how much you zoom in. This is called self-similarity. Because a coastline acts like a fractal, measuring it with a finer tool adds up all the tiny zig-zags. Theoretically, if you could measure every atom, the length would be almost infinite.
Measuring the Coast of Great Britain
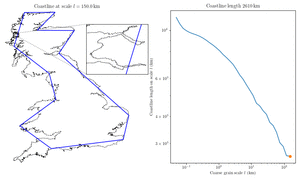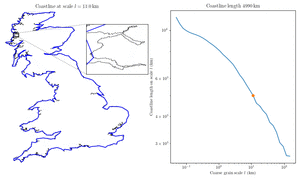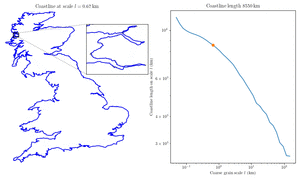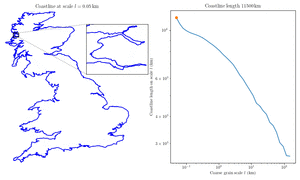
In 1967, Mandelbrot published a famous paper titled "How Long Is the Coast of Britain?". He showed that the length changes based on the unit of measurement.
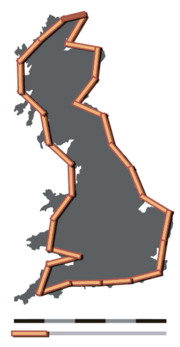
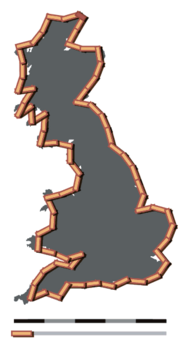
Imagine measuring an island with a straight stick:
- If you use a stick that is 100 kilometres (62 mi) long, you skip over large bays. The total length might be 2,800 kilometres (1,700 mi).
- If you use a stick that is 50 kilometres (31 mi) long, you fit into more curves. The total length grows to 3,400 kilometres (2,100 mi).
The smaller your measuring unit, the longer the coastline becomes. This means it is impossible to give a single, exact number for the length of a coastline without stating the scale used.
Real-Life Challenges
The coastline paradox causes practical problems for mapmakers and governments.
- Borders: Countries need to know exactly where their territory ends.
- Records: It is hard to say which country has the longest coastline because it depends on how it is measured.
- Environment: Scientists monitoring erosion need to agree on how to measure the shore to see if it is changing.
To solve this, experts usually agree on a specific standard or "scale" when comparing coastlines. Modern technology like GPS helps, but the definition of where the "line" is between land and water is still difficult because of tides and waves.
See also
In Spanish: Paradoja de la línea de costa para niños
- Fractal dimension
- List of countries by length of coastline
- Scale (geography)
- Zeno's paradoxes
