Four color theorem Facts for Kids

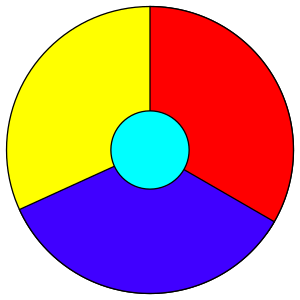
The four color theorem is a cool idea in mathematics. It says that if you have any map on a flat surface, like a piece of paper, you can color all the different areas using only four colors. The main rule is that any two areas that touch each other along a border must have different colors. If they only touch at a single point, they can have the same color.

This theorem was the first one ever to be proven with the help of a computer. It was a special kind of proof called a proof by exhaustion. This means the problem was broken down into many smaller parts, and the computer checked each one. The first proof had 1,936 parts! This was a bit controversial because people usually proved things by hand, not with a machine. Even today, the shortest proof still has over 600 parts.

Even though it's about coloring maps, most real mapmakers don't really use this theorem. Maps that only use four colors are rare, and many maps can even be colored with just three. The fourth color is sometimes needed for tricky maps, like when one area is surrounded by an odd number of other areas that all touch each other in a circle.

There's also a simpler idea called the five color theorem. It says that five colors are always enough to color any map. This one was proven much earlier and is easier to understand. Proving that *four* colors are enough was much harder! Many people tried and failed, coming up with proofs that turned out to be wrong.

What are the Rules for Coloring Maps?
History of the Four Color Problem
Why Some "Proofs" Were Wrong
Coloring Real-World Political Maps
Coloring Maps on Different Shapes
Images for kids
See also

What are the Rules for Coloring Maps?

Three colors are not enough to color this map.

Example of a map colored with four colors.

The four color theorem sounds simple, but it has some specific rules for what counts as a "map."

Every area on the map must be a single, connected piece. Think of a country like France – it's one big piece.
Areas that touch only at a single point (like the corners of four squares meeting) can have the same color. They only need different colors if they share a border line.

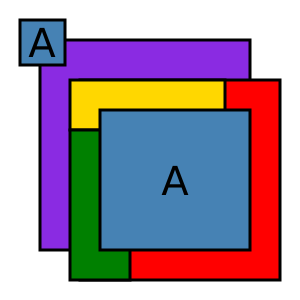
In the real world, some countries have parts that are not connected. For example, Alaska is part of the United States but is not connected to the main part. Nakhchivan is part of Azerbaijan, and Kaliningrad is part of Russia, but they are separate pieces of land. If all parts of a country must be the same color, then you might need more than four colors for a real-world map.

Example of a map of Azerbaijan with non-contiguous regions.

This map cannot be colored with four colors if the 'A' regions must be the same color.

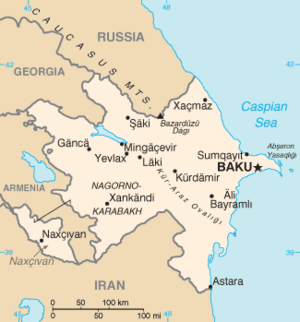
Imagine a map where two separate areas belong to the same "country" (let's call them 'A'). If both 'A' areas must be the same color, and they are surrounded by other areas that all touch each other, you might need five or even more colors. This is because the theorem assumes each "country" is one connected region.

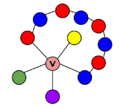
Mathematicians often think about this problem using something called graph theory. They turn the map into a "graph" where each area is a "vertex" (a point), and a line (an "edge") connects two vertices if their areas share a border. The four color theorem then says that you can color the vertices of any map-like graph with at most four colors, so no two connected vertices have the same color.

A map turned into a graph. Each circle is an area, and lines connect areas that touch.

History of the Four Color Problem

The idea of the four color theorem first came up in 1852. A law student in England named Francis Guthrie noticed that he needed at least four colors to color a map of the counties in England. He asked his brother, who then asked his math professor, Augustus De Morgan. De Morgan wrote a letter to another famous mathematician, William Rowan Hamilton, asking if four colors were always enough.

Later, in 1878, English mathematician Arthur Cayley shared the problem with other mathematicians. A year later, Alfred Kempe thought he had found a proof. But 11 years later, in 1890, Percy Heawood showed that Kempe's proof had a mistake. Another mathematician, Peter Guthrie Tait, also tried to prove it in 1880, but his proof was also shown to be wrong in 1891.

Even though Kempe's proof was wrong, he did prove something important: the Five color theorem. This theorem says that any map can be colored with no more than five colors. This was a big step, even if it wasn't the final answer for four colors.

In the 1960s and 1970s, mathematicians Heinrich Heesch, Kenneth Appel, and Wolfgang Haken started working on a proof using computers. In 1976, Appel and Haken finally announced their proof. They used a computer to check 1,936 different cases, which was a huge task! Later, they refined it to 1,476 cases.

In 1996, other mathematicians, Neil Robertson, Daniel Sanders, Paul Seymour, and Robin Thomas, made the proof even better, reducing the number of cases to 663. Again, a computer was needed to check all these cases.

In 2005, Georges Gonthier and Benjamin Werner created a "formal proof" using special computer software called Coq. This made the proof even more reliable because the software could check every tiny step.

The four color theorem is famous because it was the first major math problem to be solved with a computer's help. Some mathematicians found this unusual because they couldn't check the whole proof by hand. It also meant the proof wasn't "elegant" or simple, but it worked!

Why Some "Proofs" Were Wrong

The four color theorem has a long history of people thinking they had solved it, only to find out they were wrong. Even The New York Times newspaper was careful about reporting on the Appel–Haken computer proof because so many previous attempts had failed!

Some of the mistakes happened because people tried to create a map where one area touched all the others. This would force the remaining areas to be colored with only three colors. But because the four color theorem is true, it's always possible to color those remaining areas with three colors, even if it's tricky. The person making the "counterexample" just didn't see how.

Another common mistake was choosing some colors beforehand. If you decide certain areas *must* be a certain color, it can make it seem impossible to color the rest of the map with only four colors total. But to truly test the theorem, you have to be able to change *any* color if needed.

Also, some "false proofs" broke the rules of the theorem without realizing it. For example, they might use an area that had multiple disconnected parts, or they might not allow areas of the same color to touch at a single point, even though the theorem allows it.

Coloring Real-World Political Maps

This image shows how a torus (donut shape) can be divided into seven regions, where each region touches every other region.

In real life, political maps often have countries with exclaves or colonies (parts of a country that are separate from the main land). Since these parts must be the same color as their parent country, you often need more than four colors for a real political map. This is because these maps don't fit the "planar graph" rule that mathematicians use for the theorem.

Even though it's easy to check if a map fits the theorem's rules, finding the *fewest* number of colors needed for a complex map (especially one with disconnected parts) can be very hard. It's one of the most difficult types of problems in computer science!

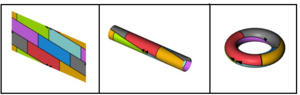
Coloring Maps on Different Shapes

The four color theorem is specifically for maps on a flat surface, like a plane or a sphere (like the surface of a globe). But what about maps on other shapes?

In 1890, Percy John Heawood (the same person who found the mistake in Kempe's proof) came up with an idea called the Heawood conjecture. It asks the same question about coloring maps, but for any kind of surface. For example, a torus (which looks like a donut) can be colored with at most seven colors. The Heawood conjecture gives a formula that works for almost all these shapes, except for one called the Klein bottle.