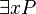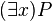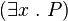Logical quantifier facts for kids

A quantifier is a special word or symbol used in logic and mathematics. It tells us how many things in a group fit a certain rule or description. For example, in the sentence "Every natural number has another natural number larger than it," the word "every" is a quantifier. It tells us that all natural numbers follow this rule.

Quantifiers help us make clear and precise statements, especially in formal languages like those used in math. They let us say exactly how common a certain quality or condition is.

The two main types of quantifiers you'll often see are:

• Universal quantifiers: These say that all or every element in a group fits a rule. The symbol for this is "∀", which looks like an upside-down "A" for "all".
• Existential quantifiers: These say that at least one element in a group fits a rule. The symbol for this is "∃", which looks like a backwards "E" for "exists".

We use quantifiers in everyday language too. Words like all, some, many, few, a lot, and no are all examples of quantifiers in English.

Quantifiers in Mathematics

Imagine you want to say something true about every natural number (like 1, 2, 3, and so on). For example, you might want to say:

1 × 2 = 1 + 1

2 × 2 = 2 + 2

3 × 2 = 3 + 3

...and so on, forever!

Writing out an infinite list like this is impossible in a formal statement, because a formal statement needs to be a certain length. This is where universal quantification comes in handy. We can shorten that endless list into one compact statement:

For each natural number n, n × 2 = n + n.

In a similar way, we can shorten an endless list of statements joined by "or," like:

1 is equal to 5 + 5, or 2 is equal to 5 + 5, or 3 is equal to 5 + 5, ...

by using existential quantification:

For at least one natural number n, n is equal to 5 + 5.

Understanding Quantifier Symbols

The two most common quantifiers are the universal quantifier (for "all") and the existential quantifier (for "at least one").

The Universal Quantifier (∀)

The universal quantifier is used to say that every element in a group meets a certain condition. We use the symbol "∀" for this. It looks like an "A" flipped upside down, standing for "all."

The Existential Quantifier (∃)

The existential quantifier is used to say that at least one element in a group meets a certain condition. We use the symbol "∃" for this. It looks like an "E" flipped backwards, standing for "exists."

We can often rewrite English sentences using these symbols, along with predicates (which describe the conditions). For example, take the sentence: "Each of Peter's friends either likes to dance or likes to go to the beach."

Let's break it down:

• Let X be the group of all Peter's friends.
• Let P(x) mean "x likes to dance."
• Let Q(x) mean "x likes to go to the beach."

Using formal notation, we can write the sentence as: 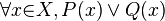. This means: "For every x that is a member of X (Peter's friends), P applies to x (they like to dance) or Q applies to x (they like to go to the beach)."

There are different ways to write these symbols in formal language, but they all mean the same thing. For example, 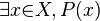(meaning "there exists an x in group X for which P is true") can also be written as:

The group of elements that a quantifier applies to is called the range of quantification or the universe of discourse. Sometimes this group is clearly stated, like "x is an apple." Then, if we write 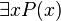, it means "at least one apple fits the condition P."

It's important to use different symbols (like x, y, z) if you are talking about different things in the same statement.

Ordering Quantifiers (Nesting)

The order of quantifiers in a statement can completely change its meaning. Let's look at an example with natural numbers:

Statement 1: For every natural number n, there exists a natural number s such that s = n².

• This statement is true. It means that every natural number has a square (e.g., 1 has 1²=1, 2 has 2²=4, 3 has 3²=9, and so on).

Now, let's swap the order of the quantifiers:

Statement 2: There exists a natural number s, such that for every natural number n, s = n².

• This statement is false. It claims that there is one single natural number s that is the square of every natural number. This isn't possible, because each natural number has its own unique square.

However, sometimes changing the order of quantifiers doesn't change the meaning. For example:

There exists a natural number x, and there exists a natural number y such that x = y².

This statement would mean the same if you swapped x and y.

Other Types of Quantifiers

While universal and existential quantifiers are the most common, mathematicians also use other types:

• Solution quantifier: This quantifier, sometimes shown with a § symbol, tells us which elements solve a particular equation. For example, means "the natural numbers n whose square is less than or equal to 4 are 0, 1, and 2."
• Counting quantifiers: These describe quantities like "many," "few," "infinitely many," or "uncountably many."
• Almost all: This means "for all but a finite number of elements."

History of Quantifiers

The idea of quantification has been around for a long time.

• Ancient Logic: Aristotle, a Greek philosopher in the 4th century BC, developed term logic. This early form of logic included quantifiers like All, Some, and No (none). His approach was closer to natural language.
• Modern Notation Begins: In 1879, Gottlob Frege created a way to write universal quantification. He didn't have a symbol for existential quantification; instead, he used universal quantification combined with negations (saying "not"). Frege's ideas became more widely known after Bertrand Russell's book Principles of Mathematics in 1903.
• Other Notations:

* In 1885, Charles Sanders Peirce and his student Oscar Howard Mitchell used Π_x for universal and Σ_x for existential quantifiers. Their notation was popular for many years. * In 1897, William Ernest Johnson and Giuseppe Peano created another notation, using (x) for universal and ∃x for existential quantification. Peano's influence helped spread this notation across Europe.

• The ∀ Symbol: The "∀" symbol for universal quantification was created by Gerhard Gentzen in 1935, but it didn't become widely used until the 1960s.

Related pages

• Determiner
• First order logic
• Rule of inference

Images for kids

• 

  Augustus De Morgan (1806-1871) was the first to use "quantifier" in the modern sense.

See also

In Spanish: Cuantificador para niños