Nonogram facts for kids

A completed nonogram of the letter W

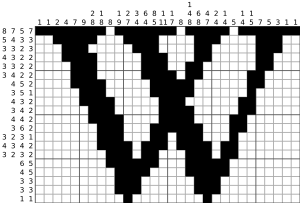
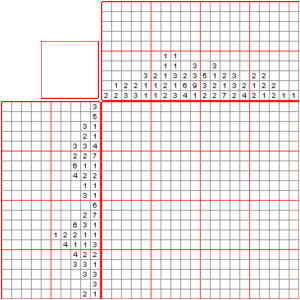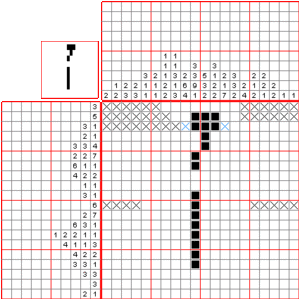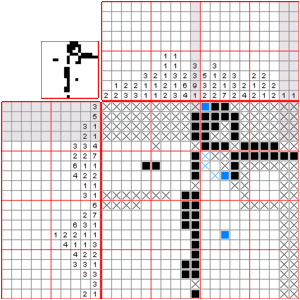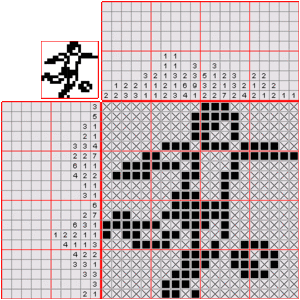
Nonograms, also known as Paint by Numbers or Picross, are fun logic puzzles where you color in squares on a grid. Your goal is to reveal a hidden picture! You figure out which squares to color and which to leave blank by following numbers given on the sides of the grid.

These numbers tell you how many groups of colored squares are in each row or column. For example, if a clue says "4 8 3", it means there are three groups of colored squares: one with four squares, then one with eight, and finally one with three. There must be at least one blank square between each group.

Most nonograms are black and white, showing a simple picture. But some can be in color! If they are, the number clues will also be colored to tell you which color to use for those squares. Sometimes, two different colored groups can be right next to each other without a blank space in between.

Nonograms can be any size and don't have to be square. They were named after Non Ishida, one of the people who invented them.

Other Names for Nonograms

Nonograms have many different names around the world! Here are some of them:

• Paint by Numbers
• Griddlers
• Pic-a-Pix
• Picross
• Hanjie
• Japanese Crosswords
• Logic Art
• Oekaki Logic

How to Play Nonograms: An Example

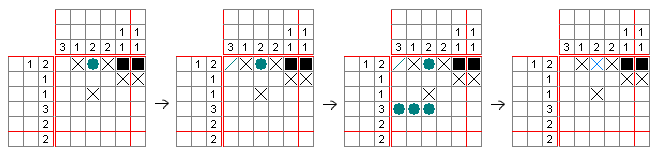
Let's look at an example to understand how nonograms work. You start with an empty grid and numbers on the sides.

The numbers on the left and top tell you how many colored squares are in each row and column. For example, if a row has the clue "4", it means there will be a group of four colored squares in that row. If it says "2 2", it means two groups of two colored squares, with at least one blank space between them.

Solving Nonograms: Smart Techniques

Example of a nonogram puzzle being solved using crosses to mark logically-confirmed spaces. Some of the steps of the process are grouped together.

To solve a nonogram, you need to figure out which squares are colored and which are empty. It's a good idea to mark empty squares with a dot or a cross. Try to use logic to fill in squares. Guessing can lead to big mistakes later on! The hidden picture isn't usually helpful for solving, but it can help you spot an error.

Many puzzles can be solved by focusing on one row or column at a time. For harder puzzles, you might need to think about what would happen if a certain square was colored or left blank. If it leads to a problem, then you know it must be the opposite!

Finding Simple Colored Squares

At the start, you can often find some squares that *must* be colored.

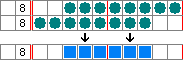
Imagine a row with 10 squares and a clue of "8". The group of 8 colored squares could start from the left, from the right, or somewhere in the middle. If you look at all the possibilities, you'll see that the middle 6 squares *have* to be colored.

This works even with more clues.

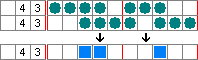
For example, in a 10-square row with clues "4" and "3":

• The group of 4 could be pushed to the far left.
• The group of 3 could be pushed to the far right.

By checking all possible spots for these groups, you can find squares that are always colored. For instance, the 3rd and 4th squares will always be part of the "4" group, and the 8th square will always be part of the "3" group.

Finding Simple Empty Squares

You can also find squares that *must* be empty.

Let's say you have a 10-square row with colored squares at the 4th and 9th positions, and clues "3" and "1".

• The clue "1" is already completed by the 9th square. This means the squares next to it (on both sides) must be empty.
• The clue "3" must include the 4th square. This means the group of 3 squares can only fit in certain spots around the 4th square. Any squares outside these possible spots must be empty.

Forcing Squares

Sometimes, placing an empty square can force other squares to be colored or empty.

Imagine a 10-square row with empty squares at the 5th and 7th positions, and clues "3" and "2".

• The "3" group would be forced to the left because it can't fit anywhere else.
• The space between the 5th and 7th empty squares (the 6th square) is too small for either a "2" or "3" group. So, the 6th square must also be empty.
• The "2" group will then be forced into a specific spot on the right, similar to the "Simple Boxes" method.

The "Glue" Technique

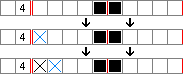
If a colored square is near the edge of the grid, and its distance from the edge is less than or equal to the first clue's number, that clue will "glue" to the edge.

For example, in a 10-square row with a colored square at the 3rd position and a clue of "5": The "5" group must include the 3rd square and will extend towards the edge, filling squares up to the 5th position.

This technique can also work in the middle of a row if an empty square acts like a border.

Joining and Splitting Groups

Sometimes, colored squares that are close together can either join to form one big group or be split by an empty square into separate groups.

Consider a 15-square row with colored squares at 3, 4, 6, 7, 11, and 13, and clues "5", "2", and "2".

• The "5" clue will join the first two colored groups (at 3-4 and 6-7) because if there was an empty square between them, it would create a group of only 4 squares, which isn't enough for a "5" clue.
• The "2" clues will split the last two colored groups (at 11 and 13) with an empty square. If they joined, it would make a group of 3, which isn't allowed for a "2" clue.

Punctuating with Empty Squares

It's very important to mark empty squares around any group of colored squares that you've completed or fully figured out. This helps you find more forced squares and is key to finishing the puzzle.

The "Mercury" Technique

This is a special way to find empty squares. If you have a colored square in a row, and it's as far from the edge as the number of the first clue, then the very first square in that row must be empty. This is because the first clue group wouldn't fit to the left of that colored square; it would have to start at or after it.

Finding Problems (Contradictions)

For harder puzzles, you might need to try out a possibility and see if it leads to a problem. It's good to use a pencil for this! 1. Pick an empty square and imagine it's colored (or empty). 2. Try to solve as much of the puzzle as you can with this assumption. 3. If you find a mistake or something that doesn't make sense, then your first guess was wrong. The square you started with must be the opposite (if you thought it was colored, it must be empty, and vice versa).

This method can be tricky because it's hard to know which square to try first. Good squares to start with are often:

• Squares with many colored neighbors.
• Squares near the edges or near groups of empty squares.
• Squares in rows that already have many colored squares.

Nonograms and Computers

Solving nonogram puzzles can be very hard for computers, especially big ones. It's known as an "NP-complete" problem. This means that there isn't a super-fast way for a computer to solve *all* nonograms quickly, unless a major math problem called "P = NP" is solved.

However, simpler nonograms, like those where each row or column only has one group of colored squares, can be solved much faster by computers.

Nonogram Video Games

Nintendo has made many popular nonogram video games under the name "Picross".

• The first Mario's Picross game came out in Japan in 1995 for the Nintendo Game Boy. It had puzzles that got harder as you played. You had a time limit and got penalties for mistakes.
• Later games like Picross 2 and Mario's Super Picross added "Wario's Picross" mode, which was even harder! In this mode, you didn't get hints, and mistakes weren't shown, so you had to be very careful.
• Nintendo also released many Picross volumes in Japan with puzzles featuring characters like Mario, Zelda, and Pokémon.
• More recently, games like Picross DS for the Nintendo DS and Picross 3D for the DS and Nintendo 3DS have been released. These games often let you download new puzzles online.
• There's even a free-to-play Pokémon-themed nonogram game called Pokémon Picross for the Nintendo 3DS.

Other companies also make nonogram video games for different devices like iOS (for iPhones and iPads) and Microsoft Windows computers.

Other Picture Logic Puzzles

There are other cool puzzles similar to nonograms that also reveal a picture!

• Pentomino paint-by-numbers uses special shapes called pentominoes (made of five squares) that you place on the grid without them touching.
• Triddlers are like nonograms but use triangles instead of squares.
• Paint by pairs or Link-a-Pix has numbers in some squares. You connect pairs of matching numbers with a line, and the line must cover exactly that many squares. When you're done, the lines form a picture.
• Fill-a-Pix has numbers in squares that tell you how many of the squares around them (including themselves) should be colored. For example, a "9" means all 8 surrounding squares and the center square are colored.
• Maze-a-Pix is a maze puzzle. When you find the correct path from start to finish, the squares that make up the path are colored to reveal a picture.

See also

In Spanish: Nonograma para niños