P versus NP facts for kids

P versus NP is a big question for people who work with computers and mathematics. It asks: If a computer can quickly check the answer to a problem, can it also quickly find the answer itself?

Let's think of it this way:

• P problems are like puzzles that are fast for computers to solve. We call these "easy" for computers.
• NP problems are like riddles. It might be hard for a computer to figure out the answer, but once someone tells the computer the answer, it's very fast and "easy" for the computer to check if that answer is correct.

In 1956, a famous mathematician named Kurt Gödel wrote a letter asking about a problem similar to this. Later, in 1971, Stephen Cook officially introduced the P versus NP problem.

Today, many people think this is the most important unsolved problem in computer science. It's one of the seven Millennium Prize Problems. The Clay Mathematics Institute offers a US$1,000,000 prize to the first person who finds the correct solution!

What Does P Versus NP Mean?

Imagine you have a tough math problem. Someone tells you, "The answer is 1, 2, 3, 4, 5." A computer can quickly check if this answer is right. But it might take the computer a very long time to figure out "1, 2, 3, 4, 5" on its own.

For some important problems, we don't know a fast way to find the answer. But if someone gives us an answer, we can check it super fast. This is why NP problems are like riddles: it's hard to guess the answer, but once you hear it, it seems obvious. The big question is: Are these riddles really as hard as we think, or are we just missing a clever trick?

Because these questions are so important for real-world uses, many mathematicians, scientists, and computer programmers want to prove that every problem that can be checked quickly can also be solved quickly. The Clay Mathematics Institute will give $1,000,000 to anyone who can prove this!

All P problems are also NP problems. This is because if a problem is easy to solve (P), it's also easy to check the answer. But the big question is: Are there any NP problems that are NOT P problems? Or are all NP problems actually P problems?

• If P is NOT equal to NP (P ≠ NP), it means some problems are truly hard to solve quickly, even if their answers are easy to check.
• If P IS equal to NP (P = NP), it means new, super-fast ways to solve these "hard" problems exist. We just haven't found them yet!

Most experts believe that P is not equal to NP. This is because smart scientists and mathematicians have tried for a long time to find fast ways to solve NP problems, but they haven't succeeded. If P = NP were proven true, it would change many parts of our daily lives in huge ways!

An Example: The Rock Problem

Let's say you want to build two towers using rocks of different weights. You want both towers to have exactly the same total weight. This means you need to divide the rocks into two piles that weigh the same.

If you guess a way to divide the rocks, it's easy to check if you're right. You just put the two piles on a balance scale to see if they weigh the same. Because it's easy to check, this "Partition" problem is an NP problem.

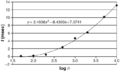
But how hard is it to solve this problem from scratch? If you have just 100 rocks, there are about 633,825,300,114,114,700,748,351,602,687 ways to divide them into two piles. That's a huge number! It's about 6.3 followed by 29 zeros.

If you could check one way to divide the rocks every day, it would take you about 1.3 followed by 22 zeros years. To compare, scientists believe the universe is only about 1.4 followed by 10 zeros years old. That means you would need to check more than two trillion (2,000,000,000,000) different ways of dividing the rocks every second since the beginning of the universe to check them all!

Even if you programmed a powerful computer to test a million ways per second, you would still need two million very powerful computers, working since the universe began, to test all the ways.

However, maybe there's a clever method to divide the rocks without checking every single combination. The question "Is P equal to NP?" is asking if such a clever, fast method can exist for problems like this.

Why This Question Matters

There are many important NP problems that people don't know how to solve quickly, other than by testing every possible answer. Here are some examples:

• A travelling salesman wants to visit 100 cities. He has limited gasoline. Can he visit all cities without running out of fuel?
• A school needs to schedule final exams for 100 classes. Students taking more than one class can't have exams at the same time. Can all exams be scheduled in one day?
• A farmer has 100 watermelons of different weights. Each box can hold 20 kilograms. Are 10 boxes enough to carry all watermelons to the market?
• An art gallery has many paintings. The owner wants to buy cameras to watch them. Are 100 cameras enough to see every painting?
• The clique problem: A school principal has a list of friends. She wants to find the largest group of students where everyone in the group is friends with everyone else.

Exponential Time: Why It's So Hard

In the rock example, with n rocks, there are about 2 to the power of n ways to divide them. The function 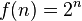is called an exponential function. It's important because it shows how the time needed to solve a problem can grow incredibly fast.

For hard problems, the solutions often need about 2 to the power of n calculations. Even if you find a way to do only 1% of these calculations, it's still a huge number. And every extra rock still doubles the number of calculations needed!

Let's look at the exam scheduling problem. Suppose it takes one hour to schedule exams for 15,000 students. If there are 10 more students (15,010 total), the time might increase by 2 to the power of 10. That's 1,024 hours, or about 6 weeks!

If there were 20 more students (15,020 total), it would take 2 to the power of 20 hours. That's 1,048,576 hours, which is about 43,691 days, or roughly 113 years!

As you can see, exponential functions grow extremely fast. Most mathematicians believe that the hardest NP problems require this kind of "exponential time" to solve.

NP-Complete Problems

Mathematicians have found a special group of NP problems called NP-Complete problems. These are the "hardest" NP problems.

Here's why they're special: If someone found a fast way to solve any one NP-Complete problem, they could use that same method to solve every single NP problem quickly! All the examples listed above (travelling salesman, exam scheduling, rock problem) are NP-Complete. So, if the salesman found a fast way to plan his trip, that same method could help the teacher schedule exams, the farmer pack watermelons, and you build your rock towers.

Because solving one NP-Complete problem means solving them all, many people are trying to find such a method. However, since there are so many different NP-Complete problems, and no one has found a fast way to solve even one yet, most experts believe it's not possible to solve them quickly.

What Makes a Problem NP-Complete?

A problem is NP-Complete if it has two main features:

• It's an NP problem: You can quickly check if a solution is correct.
• It's "NP-hard": It's at least as difficult to solve as the hardest problems in NP. This means all other NP problems can be turned into this problem in a fast way.

Famous Examples

One well-known NP-Complete problem is the Boolean satisfiability problem. In 1972, Richard Karp listed 21 problems that are now famous for being NP-Complete. These include problems like the knapsack problem (packing items into a bag to get the most value without going over a weight limit) and the vertex cover problem.

Images for kids

• 

  This graph shows how long it takes to solve a knapsack problem as the problem gets bigger.

See also

In Spanish: Clases de complejidad P y NP para niños