Sheaf (mathematics) facts for kids

In mathematics, a sheaf (pronounced "sheef," plural sheaves) is a special tool. It helps mathematicians keep track of information (like sets, abelian groups, or rings) that is connected to the open sets of a topological space. Think of a topological space as a shape or a surface, and open sets as small, connected parts of that shape.

For example, for each open part of a shape, the "data" could be all the continuous functions that work on that specific open part. This data behaves in a special way:

• You can easily shrink the data to fit smaller open parts.
• If you have many small, compatible pieces of data that cover a larger open part, you can "glue" them together to form one big piece of data for the whole open part.

The study of sheaves is called sheaf theory. Sheaves are very general and abstract mathematical ideas. They are defined precisely as "sheaves of sets" or "sheaves of rings," depending on the kind of data they hold.

There are also "maps" or "morphisms" that connect one sheaf to another. Sheaves (of a certain type, like sheaves of abelian groups) and their maps on a fixed topological space form a "category." Also, if you have a continuous map between two topological spaces, there are ways to move sheaves from one space to the other. These tools are very important in sheaf theory.

Sheaves are used in many areas of mathematics, especially in algebraic and differential geometry.

• They help describe geometric structures, like a differentiable manifold (a smooth surface) or a scheme (a more general geometric object).
• They provide a way to define a very general cohomology theory. This theory helps mathematicians understand the "holes" and shapes of spaces.
• Sheaves are also used in the theory of D-modules, which helps solve differential equations.
• More advanced versions of sheaves, used in Grothendieck topology, have even found uses in mathematical logic and number theory.

What Are Sheaves?

In many areas of mathematics, structures defined on a topological space (like a smooth surface) can be naturally "localized" or "restricted" to smaller open parts. Good examples include continuous functions, differentiable functions, or vector fields. The idea that you can restrict data to smaller open parts leads to the concept of "presheaves." Sheaves are then special kinds of presheaves where local data can be "glued" together to form global data.

Presheaves: Data on Open Sets

Let's imagine a topological space, which we'll call X. A presheaf of sets on X is like a system that organizes information:

• For every open set U in X, there's a set of data, called F(U). The items in this set are called "sections" over U. If U is the whole space X, these are called "global sections."
• If you have a smaller open set V inside a larger open set U (so V is a subset of U), there's a rule to "restrict" the data from U to V. This rule is a function called `res_V,U`. If you have a piece of data s from F(U), its restriction to V is often written as `s|_V`.

These restriction rules must follow two simple conditions:

• If you restrict data from an open set U to itself, nothing changes. It's like doing nothing.
• If you have three open sets, W inside V, and V inside U, restricting data from U to W directly is the same as restricting from U to V, and then from V to W.

A common example of a presheaf is assigning to any open set U the set of all continuous real-valued functions on U. The restriction maps simply take a continuous function on U and limit it to a smaller open set V. This still results in a continuous function.

Sheaves: Gluing Local Information

A presheaf becomes a sheaf if it satisfies two extra rules. These rules ensure that local pieces of data can be uniquely combined into a larger, consistent piece of data.

1. Locality: Imagine you have an open set U and you cover it with smaller open sets, like pieces of a puzzle. If two pieces of data from F(U) look exactly the same on every single one of these smaller puzzle pieces, then those two pieces of data must be identical on the whole U. This means local information determines the global information.
2. Gluing: Now, imagine you have a collection of data pieces, one for each small puzzle piece covering U. If all these data pieces are "compatible" (meaning they match up perfectly where their puzzle pieces overlap), then you can always "glue" them together to form one unique piece of data for the entire U.

The piece of data created by "gluing" is unique because of the locality rule. If two pieces of data satisfy the agreement condition, they are called "compatible." So, the two rules together mean that any compatible collection of local data can be uniquely glued together.

The example of continuous functions mentioned earlier is a sheaf. If you have continuous functions on small overlapping regions that match up, you can always glue them into one unique continuous function on the whole region.

However, not all presheaves are sheaves. For instance, if you assign to each open set U the set of constant real-valued functions on U, this is usually not a sheaf. Why? Because if you have a large open set U made of two separate pieces, you could have one constant value on one piece and a different constant value on the other. These won't "glue" into a single constant function on U.

Sheaves are often written with fancy capital letters like 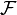(pronounced "F-script") or just F.

Examples of Sheaves

Sheaf of Sections of a Continuous Map

Imagine a continuous map f that takes points from a space Y to a space X. We can define a sheaf on X where, for any open set U in X, the sheaf gives you all the ways to "cut" through Y above U such that if you follow the cut and then apply f, you end up back in U. These "cuts" are called "sections." This is why the data elements in a sheaf are generally called sections. This idea is very important when f is like a projection from a fiber bundle (a space that looks like a product of two spaces locally) onto its base space.

For example, the sheaf of smooth functions on a manifold (a smooth surface) is a sheaf of sections.

Skyscraper Sheaf

Imagine a single point x in your space X and a group of numbers S. The "skyscraper sheaf" at x is defined like this:

• If an open set U contains x, the sheaf gives you the group S.
• If an open set U does not contain x, the sheaf gives you just the number zero (the trivial group).

The restriction maps are either the identity (if both sets contain x) or map everything to zero. It's like a skyscraper: all the action is at one point, and nowhere else.

Sheaves on Manifolds

On a smooth surface (called a manifold), there are many important sheaves:

• The sheaf of smooth functions: For any open set, this sheaf gives you all the smooth functions on that set.
• The sheaf of non-zero smooth functions.
• The sheaf of differential forms (which are used in calculus on manifolds).

In all these cases, the restriction rules are simply taking a function or form defined on a larger open set and limiting it to a smaller one.

How Sheaves Work Together

Morphisms: Maps Between Sheaves

Just like you can have functions between sets, you can have "morphisms" (or maps) between sheaves. A morphism from sheaf F to sheaf G means that for every open set U, there's a map from F(U) to G(U). This map must also be compatible with the restriction rules. This means if you take data from F(U), map it to G(U), and then restrict it to a smaller set V, it's the same as restricting the original data in F(U) to F(V) first, and then mapping it to G(V).

For example, taking the derivative is a morphism of sheaves on the real line. If you have a smooth function on an open set, its derivative is also a smooth function. And if you restrict the original function to a smaller set, taking its derivative gives the same result as taking the derivative first and then restricting.

Sheaves (of a specific type) on a fixed topological space, along with their morphisms, form a "category." This allows mathematicians to use powerful tools from category theory to study sheaves.

Stalks: What Happens at a Point?

The "stalk" of a sheaf at a point x tells you what the sheaf looks like "around" that point. It's like zooming in closer and closer to x. The stalk is defined by looking at the data on smaller and smaller open neighborhoods of x. An element of the stalk is a piece of data defined on some open neighborhood of x. Two such pieces of data are considered the same if they match up on an even smaller neighborhood.

The stalk helps us understand the local properties of a sheaf. For example, if you know the stalks of a sheaf, you can often figure out if a map between sheaves is an "isomorphism" (meaning they are essentially the same).

Turning a Presheaf into a Sheaf

Sometimes you have a presheaf that isn't quite a sheaf (it fails the gluing or locality rules). There's a way to "fix" it and turn it into the "best possible" sheaf that contains the original presheaf's information. This process is called "sheafification."

For example, the "constant presheaf" (which assigns the same set of numbers to every open set) is usually not a sheaf. Its sheafification is called the "constant sheaf." Even though it's called "constant," its sections are actually "locally constant" functions, meaning they are constant on small pieces, but not necessarily on the whole space.

Subsheaves and Quotient Sheaves

Just like you can have subsets of a set, you can have "subsheaves" of a sheaf. If you have a subsheaf, you can also form a "quotient sheaf," which is like dividing one sheaf by another. These ideas are important for building more complex sheaves from simpler ones.

Moving Sheaves Around: Pushforward and Pullback

Sheaves are tied to their specific topological space. But if you have a continuous map f between two topological spaces, say from X to Y, you can "move" sheaves between them:

Direct Image (Pushforward)

The "direct image" or "pushforward" takes a sheaf 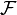on X and creates a new sheaf on Y. For any open set V in Y, the pushforward sheaf gives you the data of 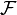on the part of X that maps into V (which is f^-1(V)). This is how the skyscraper sheaf is created.

Inverse Image (Pullback)

The "inverse image" or "pullback" goes the other way. It takes a sheaf 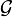on Y and creates a sheaf on X. If f is just the inclusion of an open subset, the inverse image is simply restricting the sheaf to that subset. For more general maps, it's a bit more complex, but the idea is similar: it brings the information from Y back to X.

Sheaf Cohomology: Measuring "Holes"

Sheaf cohomology is a powerful tool that uses sheaves to measure how "non-exact" certain operations are. Think of it as a way to understand when local information cannot be perfectly glued into global information.

For example, consider the exponential map for complex numbers. For any non-zero complex number, you can find its logarithm. But if you have a non-zero holomorphic function (a special kind of complex function) on a complex space, you can find its logarithm "locally" (on small pieces). However, you might not be able to find a single logarithm that works for the entire function globally. Sheaf cohomology helps us understand this "failure" to glue globally.

Sheaf cohomology groups (like H¹, H², etc.) give numbers that tell us about these "holes" or "obstructions" to gluing. The first cohomology group, H¹, specifically measures when a map between sheaves is not "surjective" (meaning not every element in the target sheaf can be reached by mapping from the source sheaf), even if it seems to be locally.

There are different ways to calculate sheaf cohomology, often by breaking down complex problems into simpler ones. For example, on smooth surfaces, the cohomology of the constant sheaf (which represents basic topological information) can be found using de Rham cohomology, which relates to differential forms.

Another common method is Čech cohomology, which uses the way open sets cover a space to compute these groups. It's often used for practical calculations.

History of Sheaves

The idea of sheaves slowly developed over time, starting in the 1930s and becoming a distinct field by the 1950s.

• 1936: Eduard Čech introduced a way to connect open coverings of a space to a geometric object called a "simplicial complex," which was an early step.
• 1945: Jean Leray, while a prisoner of war, developed early ideas related to sheaves and "spectral sequences" to solve problems in PDE theory.
• 1947-1950: Henri Cartan and his seminar in Paris began to formalize sheaf theory, defining the "sheaf space" (or "étalé space") and introducing concepts like "supports" and "cohomology with supports."
• 1951: The Cartan seminar proved important theorems (theorems A and B) based on the work of Kiyoshi Oka in complex analysis.
• 1954: Jean-Pierre Serre introduced sheaves into algebraic geometry with his paper "Faisceaux algébriques cohérents" (Coherent Algebraic Sheaves). This was a major turning point.
• 1955: Alexander Grothendieck, a very influential mathematician, redefined sheaf cohomology using "derived functors," making it applicable to all topological spaces.
• 1957 onwards: Grothendieck continued to expand sheaf theory to meet the needs of algebraic geometry, introducing concepts like schemes, local cohomology, and Grothendieck topologies. These ideas were crucial for solving the Weil conjectures in number theory.

By the late 1950s, sheaves had become a fundamental part of mathematics, used in many fields beyond just algebraic topology.