Symmetry (geometry) facts for kids

A drawing of a butterfly with bilateral symmetry, with left and right sides as mirror images of each other.

In geometry, an object has symmetry if it looks exactly the same after you do something to it, like flipping it or turning it. Imagine a butterfly: if you draw a line down its middle, one side is a perfect mirror image of the other. That's a type of symmetry!

A circle is another great example. If you spin a circle around its center, it still looks like the same circle. We say a circle has 'rotational symmetry' because it stays the same when rotated.

What are Geometric Symmetries?

Geometric symmetries are about how shapes and objects can be moved or changed but still look exactly the same. These movements are called "transformations." The most common transformations are:

• Reflections: Flipping an object over a line or plane, like looking in a mirror.
• Rotations: Turning an object around a point or axis.
• Translations: Sliding an object from one place to another without turning or flipping it.

If an object looks the same after one of these transformations, it has that type of symmetry.

Reflectional Symmetry

In 2 dimensions, a point reflection is a 180 degree rotation.

Reflectional symmetry, also known as mirror symmetry or bilateral symmetry, is when an object can be divided by a line or a plane, and one side is a perfect mirror image of the other.

• In 2D shapes, this dividing line is called an axis of symmetry. If you fold the shape along this line, both halves match up perfectly.
  • For example, a square has four axes of symmetry. You can fold it in four different ways, and its edges will line up.
  • A circle has endless axes of symmetry, all passing through its center.
• In 3D objects, this is called a plane of symmetry. Imagine cutting an apple in half; if both halves are identical, it has a plane of symmetry.

Some letters, like 'T' or 'A', have vertical reflectional symmetry. If you flip them over a vertical line, they look the same. Triangles that have reflection symmetry are called isosceles triangles.

A special type of reflection is a point reflection. In 2D, this is like rotating an object 180 degrees around a central point. The object ends up upside down but still looks the same.

Rotational Symmetry

The triskelion has 3-fold rotational symmetry.

Rotational symmetry means an object looks the same after you turn it around a central point or axis.

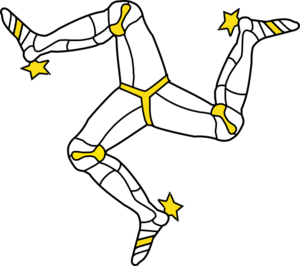
• The triskelion symbol, like the one on the flag of the Isle of Man, has 3-fold rotational symmetry. This means if you turn it 120 degrees (one-third of a full circle), it looks exactly the same.
• A square has 4-fold rotational symmetry because it looks the same after turning 90, 180, 270, or 360 degrees.
• A circle has infinite rotational symmetry because it looks the same no matter how little you turn it.

Rotational symmetry is found everywhere, from flowers to wheels.

Translational Symmetry

A frieze pattern with translational symmetry

Translational symmetry is when an object or pattern looks the same after you slide it a certain distance in a specific direction. It's like having a repeating pattern.

Imagine a row of identical footprints on a beach. If you slide the whole row so that one footprint moves exactly into the spot of the next one, the entire row looks unchanged. If this row went on forever, it would have translational symmetry.

This type of symmetry is common in patterns like wallpaper designs or frieze patterns (patterns that repeat along a strip).

Glide Reflection Symmetry

A frieze pattern with glide reflection symmetry

Glide reflection symmetry is a bit more complex. It's a combination of two movements: 1. A reflection (flipping over a line). 2. A translation (sliding along that same line).

Think about footprints again, but this time, imagine walking. Your left foot steps, then your right foot steps. The pattern of footprints on the ground shows glide reflection symmetry. Each right footprint is a reflection of a left footprint, but also shifted forward.

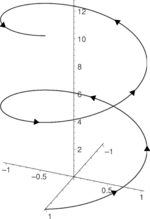
Helical Symmetry

A continuous helix

Helical symmetry is found in objects that look like spirals or screws. Think of a spring, a drill bit, or a Slinky toy.

An object with helical symmetry looks the same if you rotate it around its central axis AND slide it along that axis at the same time. It's like moving along a spiral staircase.

There are different types of helical symmetry:

• Infinite helical symmetry: This is for objects like a perfectly coiled spring that looks the same no matter how much you rotate and slide it.
• N-fold helical symmetry: This is when the pattern repeats after a specific rotation and slide, like the two strands of a double helix.
• Non-repeating helical symmetry: In some cases, the rotation needed to see the symmetry never repeats perfectly. DNA is an example, with about 10.5 base pairs per turn.

Scale Symmetry and Fractals

A Julia set has scale symmetry

Scale symmetry means that if you make an object bigger or smaller, it still looks the same or has the same properties. This is also called self-similarity.

You can see this in nature:

• A fern leaf has smaller leaves that look like tiny versions of the whole leaf.
• The branching of a tree looks similar whether you're looking at the whole tree or just a small twig.
• A coastline, when viewed from space or up close, often shows similar jagged patterns.

A more complex form of scale symmetry is found in fractals. Fractals are mathematical shapes where the same complex pattern repeats at every level of magnification. The Mandelbrot set is a famous example. Fractals are used in computer graphics to create realistic natural scenes, like mountains or clouds, because they look so much like patterns found in nature.

Images for kids

• 

  A regular skew-apeirogon has a discrete (3-fold here) screw-axis symmetry, drawn in perspective.

• 

  The Boerdijk–Coxeter helix, constructed by augmented regular tetrahedra, is an example of a screw axis symmetry that is nonperiodic.

• 

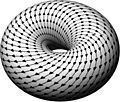
  A 4D clifford torus, stereographically projected into 3D, looks like a torus. A double rotation can be seen as a helical path.