2,147,483,647 facts for kids
Quick facts for kids 2147483647 |
|
|---|---|
| Cardinal | two billion one hundred forty-seven million four hundred eighty-three thousand six hundred forty-seven |
| Ordinal | 2147483647th (two billion one hundred forty-seven million four hundred eighty-three thousand six hundred forty-seventh) |
| Factorization | prime |
| Prime | 105,097,565th |
| Greek numeral | 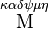 ͵γχμζ´ ͵γχμζ´ |
| Binary | 11111111111111111111111111111112 |
| Ternary | 121121222121102021013 |
| Senary | 5530320055316 |
| Octal | 177777777778 |
| Duodecimal | 4BB2308A712 |
| Hexadecimal | 7FFFFFFF16 |
The number 2,147,483,647 is a very special number in mathematics and computing. It is known as the eighth Mersenne prime. A Mersenne prime is a prime number that is one less than a power of two. This number is equal to 231 − 1.
This number is also important because it is the largest positive number that a computer can store using a common way called a "signed 32-bit integer."

Contents
Discovering This Special Prime
A famous mathematician named Leonhard Euler proved that 2,147,483,647 is a prime number. A prime number is a whole number greater than 1 that can only be divided evenly by 1 and itself. Euler shared his proof in a letter in 1772.
At that time, this number was the largest known prime number. It held this record for a very long time, until 1867.
A Prediction About Big Numbers
When 2,147,483,647 was discovered, it was the biggest prime number anyone knew. In 1811, a mathematician named Peter Barlow wrote something interesting. He thought that this number was probably the biggest prime number that would ever be found. He believed people wouldn't try to find bigger ones because they weren't "useful."
However, Barlow was wrong! People did keep looking for bigger prime numbers. A larger prime was found in 1855, and another was proven in 1867.
How Computers Use This Number
The number 2,147,483,647 is very important in how computers work. It is the highest positive number that a 32-bit signed binary integer can hold. Think of it as the maximum value for many numbers stored in computer programs.
Sometimes, if a computer program tries to go over this limit, it can cause problems. This is called an overflow. It can make a program act strangely or even crash.
The Year 2038 Problem
Many computer systems, especially older ones, use a 32-bit integer to keep track of time. They count the number of seconds that have passed since January 1, 1970.
The maximum number of seconds these systems can count is 2,147,483,647. This means that on Tuesday, January 19, 2038, at 03:14:07 UTC, these systems will run out of numbers. This event is known as the Year 2038 problem. It could cause issues for computers that rely on this way of counting time.
Computer Bugs and This Number
Sometimes, this number can cause unexpected computer problems. For example, on January 1, 2022, some Microsoft Exchange email systems had a bug. Their internal scanner used a 32-bit integer for the date and time. When the year changed, the number became too big for the system to handle. This caused email delivery to stop working for a while.
In Video Games
This number often shows up as a limit in video games. If a game uses a 32-bit signed integer to store things like points, money, or item counts, then 2,147,483,647 becomes the highest possible value.
If a player tries to get more than this amount, strange things can happen:
- Wrapping: The number might "wrap around" and become a negative number.
- Crashing: The game might crash because it doesn't know how to handle a number bigger than its limit.
A well-known example is in games like Old School RuneScape and Grand Theft Auto V. In these games, 2,147,483,647 is the maximum amount of coins or items a player can hold. This is often called a "max cash stack."
Sometimes, games use an "unsigned" 32-bit integer. This type of integer can only store positive numbers, but it can go up to a larger limit: 4,294,967,295.
See also
 In Spanish: 2147483647 para niños
In Spanish: 2147483647 para niños

