Cryptanalysis of the Lorenz cipher facts for kids
The cryptanalysis of the Lorenz cipher was how British codebreakers secretly read important German army messages during World War II. The British Government Code and Cypher School (GC&CS) at Bletchley Park decoded many messages. These messages were sent between the German High Command (called Oberkommando der Wehrmacht, or OKW) in Berlin and their army groups across Europe. Some messages were even signed by Adolf Hitler.
These messages were not sent using Morse code. Instead, they were scrambled by special machines called Lorenz SZ teleprinter cipher machines. Decoded messages from this system became a very important source of secret information called "Ultra" intelligence. This information greatly helped the Allies win the war.
For their top-secret messages, the German army used these "secret writer" (Geheimschreiber) machines. They scrambled each letter using a 5-bit code called ITA2. The main machine used by the army was the Lorenz SZ (SZ means "cipher attachment"). The air force used the Siemens and Halske T52.
Codebreakers at Bletchley Park found out that the Germans called one of their wireless teleprinter systems "Sägefisch" (sawfish). So, the British codebreakers started calling the German encrypted radio messages "Fish". The first non-Morse link they found was named "Tunny" (tunafish). This name was then used for the cipher machines and their messages.
Just like with the Enigma machine, the Germans made mistakes in how they used the Lorenz machines. These mistakes helped the British figure out how the system worked. Unlike the Enigma, the Allies didn't get their hands on a physical Lorenz machine until the very end of the war. By then, they were already decoding messages regularly. The challenge of decoding Tunny messages led to the invention of "Colossus". This was the world's first electronic, programmable digital computer. By the end of the war, ten Colossus computers were in use. They helped Bletchley Park decode about 90% of the important Tunny messages.
Albert W. Small, an American codebreaker who worked on Tunny at Bletchley Park, wrote in 1944:
Daily solutions of Fish messages at GC&CS reflect a background of British mathematical genius, superb engineering ability, and solid common sense. Each of these has been a necessary factor. Each could have been overemphasised or underemphasised to the detriment of the solutions; a remarkable fact is that the fusion of the elements has been apparently in perfect proportion. The result is an outstanding contribution to cryptanalytic science.
| Time | Event |
|---|---|
| September 1939 | World War II begins in Europe. |
| Second half of 1940 | First non-Morse messages are found. |
| June 1941 | First test SZ40 Tunny link starts. |
| August 1941 | Two long messages with the same settings give 3700 characters of key. |
| January 1942 |
|
| July 1942 |
|
| October 1942 |
|
| November 1942 | The "1+2 break in" method is invented by Bill Tutte. |
| February 1943 | More complex SZ42A machine is introduced. |
| May 1943 | Heath Robinson machine is delivered. |
| June 1943 | Newmanry section is founded. |
| December 1943 | Colossus I works at Dollis Hill before moving to Bletchley Park. |
| February 1944 | First use of Colossus I for real work. |
| March 1944 | Four Colossus Mark 2 machines are ordered. |
| April 1944 | Order for more Colossus machines increases to 12. |
| June 1944 |
|
| August 1944 | Cam settings on all Lorenz wheels change daily. |
| May 1945 |
|
Contents
German Tunny Machines
The Lorenz SZ cipher machines used a type of cipher called a Vernam stream cipher. They had a complicated set of twelve wheels that created a very long, random-like sequence of characters. This sequence was called the "key stream". The key stream was combined with the original message (plaintext) to create the scrambled message (ciphertext). At the other end, an identical machine with the same settings would create the same key stream. This key stream was then combined with the scrambled message to get the original message back. This is called a symmetric-key system.
Ten of the twelve wheels created the key stream. This was done by mixing the 5-bit character from the five right-hand wheels (called chi wheels) with the 5-bit character from the five left-hand wheels (called psi wheels). The chi wheels always moved one step forward for every character. But the psi wheels did not always move.
The two middle wheels (called "motor" wheels) decided if the psi wheels would turn with a new character. After each letter was scrambled, either all five psi wheels moved, or they stayed still. The motor wheel with 61 cams moved after every character. If its cam was in the "active" position, the other motor wheel (with 37 cams) moved. If it was in the "inactive" position, the 37-cam wheel and the psi wheels stayed still. Later machines had more complex rules for when the psi wheels moved.
The Lorenz SZ42 machines had a total of 501 cams on their twelve wheels. These numbers were all co-prime (meaning they shared no common factors other than 1). This made the key sequence extremely long before it repeated. Each cam could be either "raised" (active) or "lowered" (inactive). A raised cam changed the value of a bit. The total number of possible cam patterns was huge. In reality, about half the cams on each wheel were raised. The Germans later realized that if the number of raised cams wasn't close to 50%, it could create weaknesses.
At Bletchley Park, figuring out which of the 501 cams were raised was called "wheel breaking". Finding the starting positions of the wheels for a specific message was called "wheel setting". The fact that the psi wheels moved together, but not with every character, was a big weakness that helped the British codebreakers.

Secure Telegraphy
Electro-mechanical telegraphy was invented in the 1830s and 1840s, long before telephones. It was used worldwide by World War II. A huge system of cables connected places within and between countries. When cables weren't practical, like for mobile German army units, radio was used.
Teleprinters at each end of the circuit had a keyboard and a printer. They often also had a way to read and punch holes in paper tape. When used "online," typing a letter on one machine would print it on the other. But often, operators would prepare messages offline by punching them onto paper tape. Then they would go online only to send the messages from the tape. This was faster, sending about ten characters per second.
Messages were represented by codes from the International Telegraphy Alphabet No. 2 (ITA2). The transmission used a system where each character was signaled by a start impulse, 5 data impulses, and 1½ stop impulses. At Bletchley Park, "mark" impulses were shown as `x` and "space" impulses as `•`. For example, the letter "H" was coded as `••x•x`.
The "figure shift" (FIGS) and "letter shift" (LETRS) characters told the receiving machine how to interpret the following characters. Because a shift character could get corrupted, some operators would type two shift characters when changing from letters to numbers or vice versa. For example, they might type `55M88` for a full stop. This doubling of characters was very helpful for the statistical analysis used at Bletchley Park. After scrambling, shift characters had no special meaning.
Radio-telegraph messages were sent three or four times faster than Morse code. A human listener could not understand them. However, a standard teleprinter would print the message. The Lorenz cipher machine changed the original message into a scrambled message that only someone with an identical machine, set up in the exact same way, could read. This was the challenge for the Bletchley Park codebreakers.
Intercepting Tunny Messages
Intercepting Tunny messages was very difficult. The German transmitters sent signals in specific directions, so most signals were quite weak in Britain. Also, the Germans used about 25 different radio frequencies for these messages, and they sometimes changed the frequency during a transmission. After finding these non-Morse signals in 1940, a special radio intercept station was set up at Ivy Farm in Knockholt, Kent. Its only job was to catch this traffic. This center, led by Harold Kenworthy, had 30 receiving sets and 600 staff. It was fully ready by early 1943.
Accuracy was vital because even one missed or wrong character could make decoding impossible. The "undulator" technology used to record the impulses was originally for high-speed Morse code. It made a visible record of the impulses on narrow paper tape. People called "slip readers" then read these tapes, interpreting the peaks and troughs as the marks and spaces of ITA2 characters. Then, perforated paper tape was made and sent by telegraph to Bletchley Park.
The Vernam Cipher Explained
The Vernam cipher, used by the Lorenz SZ machines, uses a special logic function called "exclusive or" (XOR). This is like saying "A or B, but not both." It's shown by the symbol ⊕.
| INPUT | OUTPUT | |
| A | B | A ⊕ B |
| • | • | • |
| • | x | x |
| x | • | x |
| x | x | • |
In this table, `x` means "true" and `•` means "false". XOR is also like addition or subtraction in modulo 2 (without carrying or borrowing).
A good cipher machine should be able to both scramble and unscramble messages using the same settings. The Vernam cipher does this. If you combine the original message (plaintext) with the key, you get the scrambled message (ciphertext). If you combine the scrambled message with the same key, you get the original message back.
- Plaintext ⊕ Key = Ciphertext
- Ciphertext ⊕ Key = Plaintext
Vernam's original idea was to use two paper tapes: one for the message and one for the key. But making and sending unique key tapes for every message was too hard. So, in the 1920s, inventors created rotor cipher machines, like the Lorenz SZ40/42, to create the key stream instead of using tapes.
How Lorenz Ciphers Were Broken
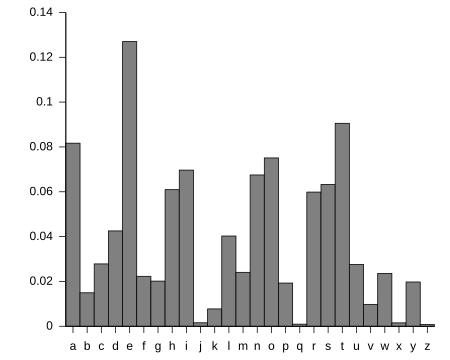
A simple cipher, like the Caesar cipher, can be easily broken if you have enough scrambled text. This is done by looking at how often each letter appears (frequency analysis) and comparing it to how often letters appear in normal language.
With a more complex cipher, like Lorenz, a frequency analysis shows that all letters appear about equally often. This makes it look like a random stream. However, because one set of Lorenz wheels (the chi wheels) turned with every character while the other set (the psi wheels) did not, the machine didn't completely hide patterns in how adjacent characters were used in the German messages. Alan Turing found this weakness and created a technique called "differencing" to use it.
The patterns of raised cams on the motor wheels were changed daily. The chi wheel patterns were changed monthly at first. The psi wheel patterns were changed every three months until October 1942, then monthly. From August 1, 1944, both chi and psi wheel patterns were changed daily.
The number of possible starting positions for the wheels was huge (about 1.6 followed by 19 zeros). This was far too many to try every single one. Sometimes, Lorenz operators made a mistake and sent two messages with the exact same starting positions. This was called a "depth". The way the transmitting operator told the receiving operator the wheel settings was called the "indicator" at Bletchley Park.
In August 1942, the Germans stopped using standard beginnings for their messages, which had been helpful for codebreakers. They replaced them with irrelevant text, called quatsch (German for "nonsense"). This made identifying the real message harder.
During the early test transmissions, the indicator was twelve German first names. The first letters of these names showed the starting positions of the twelve wheels. This helped identify "depths" (messages with the same settings) or "partial depths" (messages with only one or two different settings). From October 1942, the indicator system changed. Operators sent the unscrambled letters QEP followed by a two-digit number from a codebook. This meant that only full depths could be found when a QEP number was reused on a specific Tunny link.
Diagnosing the Tunny Machine
The first step in breaking a new cipher is to understand how it works. For Tunny, this meant figuring out the machine's logic without ever seeing one. The scrambling system was very good at making the scrambled message (ciphertext) look completely random. However, this wasn't true for the key or its parts, which was the weakness that allowed Tunny keys to be solved.
During the early test period, when the twelve-letter indicator system was used, John Tiltman, a very talented codebreaker at Bletchley Park, studied the Tunny messages. He realized they used a Vernam cipher.
When two messages (let's call them 'a' and 'b') use the same key, combining them removes the key's effect. If we call the two scrambled messages Za and Zb, the key K, and the two original messages Pa and Pb, then:
- Za ⊕ Zb = Pa ⊕ Pb
If the two original messages (plaintexts) could be figured out, the key could be recovered from either pair:
- Za ⊕ Pa = K
- Zb ⊕ Pb = K
On August 31, 1941, two long messages were received with the same indicator: HQIBPEXEZMUG. The first seven characters were the same, but the second message was shorter. John Tiltman tried guessing common German phrases (called "cribs") against the combined message (Za ⊕ Zb). He found that the first message started with the German word SPRUCHNUMMER (message number). In the second message, the operator had used the common abbreviation NR for NUMMER. There were more abbreviations in the second message, and punctuation sometimes differed. This allowed Tiltman, over ten days, to figure out the original text of both messages. This, in turn, gave him almost 4000 characters of the key.
Members of the Research Section tried to find a mathematical description of how the key was made, but they couldn't. Bill Tutte joined the section in October 1941 and was given the task. He had studied chemistry and mathematics at Trinity College, Cambridge before coming to Bletchley Park. He knew a technique called Kasiski examination, where you write out a key on squared paper in rows. If the row length matches a repeating pattern in the key, columns will show more repetitions than random chance.
Tutte thought that instead of looking at whole letters of the key, which might repeat very slowly, it might be better to look at just one bit (impulse) from each letter. He believed "the part might be cryptographically simpler than the whole." Since the Tunny indicators used 25 letters for 11 wheel positions and 23 for the twelfth, he tried Kasiski's technique on the first bit of the key characters using a repetition of 25 × 23 = 575. This didn't work well, but he saw a pattern diagonally. So, he tried 574, which showed repeats in the columns. Realizing that the prime factors of 574 are 2, 7, and 41, he tried a period of 41 and found "a rectangle of dots and crosses that was full of repetitions."
It was clear that the sequence of first bits was more complex than what a single wheel of 41 positions would produce. Tutte called this part of the key χ1 (chi). He figured there was another part, combined with this using XOR, that didn't always change with each new character. He called this the ψ1 (psi) wheel. The same applied to each of the five bits (impulses). So, for a single character, the key K had two parts:
- K = χ ⊕ ψ
The actual sequence of characters added by the psi wheels, including when they didn't move, was called the extended psi, shown as ψ′:
- K = χ ⊕ ψ′
Tutte could figure out the ψ part because dots were more likely to be followed by dots, and crosses by crosses. This was a weakness in how the Germans set their keys, which they later fixed. Once Tutte made this breakthrough, the rest of the Research Section joined in. They found that the five ψ wheels all moved together, controlled by two "motor" wheels (called μ or "mu").
Figuring out how the Tunny machine worked in this way was an amazing achievement. When Tutte was honored in 2001, it was called "one of the greatest intellectual feats of World War II."
Turingery: The Differencing Method
Alan Turing spent a few weeks in the Research Section in July 1942. He was interested in breaking Tunny using the keys they had found from "depths." He developed a way to figure out the cam settings (wheel breaking) from a piece of key. This method became known as "Turingery." It introduced the important idea of "differencing," which was key to solving Tunny messages even without depths.
What is Differencing?
Codebreakers looked for a way to change the scrambled message or key to reveal patterns that the scrambling process was supposed to hide. Turing realized that combining the values of two consecutive characters in a stream (using XOR) would highlight any patterns. The resulting stream was called the "difference" (symbolized by the Greek letter "delta" Δ). This is because XOR is the same as modulo 2 subtraction. So, for a stream of characters S, the difference ΔS was found by:
- ΔS = S ⊕ S (where underline means the next character)
This "differencing" could be applied to the scrambled message (Z), the original message (P), the key (K), or its parts (χ and ψ). The relationships between these parts still held true when they were differenced. For example:
- ΔK = Δχ ⊕ Δψ
And for the scrambled message, original message, and key parts:
- ΔZ = ΔP ⊕ Δχ ⊕ Δψ
So:
- ΔP = ΔZ ⊕ Δχ ⊕ Δψ
Differencing helped break Tunny because, even though the scrambled message looked random, a version of it with the chi part of the key removed did not. This is because when the original message had repeated characters and the psi wheels didn't move, the differenced psi character (Δψ) would be a "null" character (called '/' at Bletchley Park). When you XOR something with a null character, it doesn't change. So, in these cases, ΔK = Δχ. The scrambled message with the chi part removed was called the "de-chi" ('D).
So the "delta de-chi" (ΔD) was:
- ΔD = ΔZ ⊕ Δχ
Repeated characters in the original message were common. This was partly because of common German letter pairs (like EE, TT, LL, SS). Also, telegraph operators often repeated shift characters (like figures-shift and letters-shift) because losing one could make the message unreadable.
The "General Report on Tunny" said: "Turingery introduced the principle that the key differenced at one, now called ΔΚ, could yield information unobtainable from ordinary key. This Δ principle was to be the fundamental basis of nearly all statistical methods of wheel-breaking and setting."
Differencing was applied to each of the five bits of the ITA2 coded characters. So, for the first bit, scrambled by wheels χ1 and ψ1, differenced at one:
- ΔK1 = K1 ⊕ K1
And so on for all five bits.
The repeating patterns of the chi and psi wheels (for example, 41 and 43 for the first bit) also showed up in the pattern of ΔK. However, since the psi wheels didn't advance for every character, the pattern for ΔK1 was more complex than a simple repetition every 41 × 43 = 1763 characters.
Turing's Method for Wheel Breaking
Turing's method for finding the cam settings of the wheels from a piece of key (obtained from a depth) involved a step-by-step process. Since the delta psi character was the null character about half the time, assuming that ΔK' = Δχ had a 50% chance of being correct. The process started by treating a specific ΔK character as the Δχ for that position. The resulting pattern of `x` and `•` for each chi wheel was recorded on a sheet of paper. This sheet had columns for each character in the key and five rows for the five bits of the Δχ. Knowing the repeating patterns of each wheel from Tutte's earlier work, these values could be spread to the correct positions throughout the rest of the key.
They also prepared five sheets, one for each chi wheel. These sheets had columns for each cam on that wheel and were called a "cage." For example, the χ3 cage had 29 columns. As they made more guesses for Δχ values, they found more possible cam settings. These guesses either matched or disagreed with earlier assumptions. They kept a count of agreements and disagreements. If disagreements were much higher than agreements, they assumed the Δψ character was not the null character, and that guess was ignored. Slowly, all the cam settings of the chi wheels were figured out. From those, the psi and motor wheel cam settings could be found.
As they gained more experience, they improved the method. This allowed them to use much shorter pieces of key than the original 500 characters.
The Testery
The Testery was the section at Bletchley Park that did most of the work to decode Tunny messages. By July 1942, the number of messages was growing fast. So, a new section was created, led by Ralph Tester—which is how it got its name. The staff were mostly former members of the Research Section. The Testery's methods were almost entirely manual, even after automated machines were introduced in the Newmanry to help speed up their work.
The first phase of the Testery's work, from July to October, mainly used "depths" (messages with identical settings) and "partial depths" for decoding. After ten days, however, the Germans replaced the standard message beginnings with "nonsense" (quatsch), making decoding harder. Still, this period was productive, even though each decoding took a long time. Finally, in September, a depth was received that allowed Turing's method of wheel breaking to be used. This meant they could start reading current messages. They also gathered a lot of data about the statistical features of the German language in the messages and expanded their collection of "cribs" (likely phrases).
In late October 1942, the original test Tunny link was closed. Two new links, Codfish and Octopus, were opened. With these and later links, the 12-letter indicator system was replaced by the QEP system. This meant that only full depths (from identical QEP numbers) could be recognized, which greatly reduced the number of messages they could decode.
Once the Newmanry started working in June 1943, the Testery's work changed. Decrypting and wheel breaking no longer relied on depths.
British Tunny Machine

The "British Tunny Machine" was a device that perfectly copied what the German SZ40/42 machines did. It was used to get the original German text from a scrambled message tape, once the cam settings had been figured out. The design was created at Bletchley Park. By the end of the war, ten Testery Tunnies were in use. It was designed and built at the General Post Office Research Station at Dollis Hill by Tommy Flowers's team. It was mostly made from standard British telephone exchange parts like relays and uniselectors. Messages were put in and taken out using a teleprinter with paper tape reading and punching. These machines were used in both the Testery and later the Newmanry. Dorothy Du Boisson, a machine operator, said plugging in the settings was like using an old telephone exchange, and she sometimes got electric shocks!
When Tommy Flowers was asked to try the first British Tunny machine, he typed a standard test phrase: "Now is the time for all good men to come to the aid of the party." He was very pleased when the machine printed out a line from a Wordsworth poem:
| Input | NOW IS THE TIME FOR ALL GOOD MEN TO COME TO THE AID OF THE PARTY |
| Output | I WANDERED LONELY AS A CLOUD THAT FLOATS ON HIGH OER VALES AND H |
Extra features were added to the British Tunnies to make them easier to use. More improvements were made for the versions used in the Newmanry.
The Newmanry
The Newmanry was a section started by Max Newman in December 1942. Its goal was to find ways to help the Testery by automating parts of the Tunny message decoding process. Newman had been working with Gerry Morgan, head of the Research Section, on how to break Tunny. Then, in November 1942, Bill Tutte came to them with an idea for what became known as the "1+2 break in." They realized this could work, but only if it was automated.
Newman created a detailed plan for what would become the "Heath Robinson" machine. He got help from the Post Office Research Station at Dollis Hill and Dr C.E. Wynn-Williams at the Telecommunications Research Establishment (TRE) in Malvern to build his idea. Engineering design started in January 1943, and the first machine was delivered in June. At that time, the staff included Newman, Donald Michie, Jack Good, two engineers, and 16 Wrens (members of the Women's Royal Naval Service). By the end of the war, the Newmanry had three Robinson machines, ten Colossus Computers, and several British Tunnies. The staff grew to 26 codebreakers, 28 engineers, and 275 Wrens.
Automating these processes meant handling huge amounts of punched paper tape, like the ones with the scrambled messages. Absolute accuracy of these tapes was crucial. Even one wrong character could ruin a lot of work. Jack Good introduced the rule: "If it's not checked it's wrong."
The "1+2 Break In" Method
W. T. Tutte found a way to use the fact that certain pairs of letters (bigrams) in German text were not evenly distributed. He used the "differenced" scrambled message and key parts. His method was called the "1+2 break in," or "double-delta attack." The main idea was to find the starting settings of the chi part of the key. They did this by trying all possible combinations with the scrambled message and looking for patterns that showed the original message's characteristics. This required knowing the current cam settings from the "wheel breaking" process. It was impossible to generate all 22 million characters from all five chi wheels, so they started by looking at only the first two wheels (41 × 31 = 1271 combinations).
For each of the five impulses (bits), `i`:
- Zi = χi ⊕ ψi ⊕ Pi
Which means:
- Pi = Zi ⊕ χi ⊕ ψi
For the first two impulses:
- (P1 ⊕ P2) = (Z1 ⊕ Z2) ⊕ (χ1 ⊕ χ2) ⊕ (ψ1 ⊕ ψ2)
If they calculated a possible (P1 ⊕ P2) for each starting point of the (χ1 ⊕ χ2) sequence, they would get `x`s and `•`s. Over time, the correct starting point would show a higher proportion of `•`s. Tutte knew that using the differenced (∆) values made this effect even stronger. This is because any repeated characters in the original message would always create a `•`. Also, ∆ψ1 ⊕ ∆ψ2 would create a `•` whenever the psi wheels didn't move (about 70% of the time overall).
Tutte analyzed a decoded message using the differenced version of the function above:
- (∆Z1 ⊕ ∆Z2) ⊕ (∆χ1 ⊕ ∆χ2) ⊕ (∆ψ1 ⊕ ∆ψ2)
He found that it generated `•` about 55% of the time. Because of how the psi wheels contributed, the alignment of the chi-stream with the scrambled message that gave the highest count of `•`s from (∆Z1 ⊕ ∆Z2 ⊕ ∆χ1 ⊕ ∆χ2) was most likely the correct one. This technique could be used for any pair of impulses. It provided the basis for an automated way to get the "de-chi" (D) of a scrambled message. From there, the psi part could be removed using manual methods.
Robinsons: The First Machines
Heath Robinson was the first machine built to automate Tutte's "1+2 method." The Wrens who operated it named it after cartoonist William Heath Robinson. He drew incredibly complex machines for simple tasks, similar to the American cartoonist Rube Goldberg.
Max Newman created the machine's functional plan. The main engineering design was done by Frank Morrell at the Post Office Research Station in North London. His colleague Tommy Flowers designed the "Combining Unit." Dr C. E. Wynn-Williams from the Telecommunications Research Establishment built the high-speed electronic counters. Construction began in January 1943, and the first machine was used at Bletchley Park in June.
The main parts of the machine were:
- A tape transport and reading system (called the "bedstead" because it looked like an upright metal bed frame). This ran the looped key and message tapes at 1000 to 2000 characters per second.
- A combining unit that performed the logic of Tutte's method.
- A counting unit that counted the number of `•`s. If the count went over a set total, it would display or print it.
The first machine worked well, even with some problems. Most of these were fixed as they developed what became known as "Old Robinson."
Colossus: The First Electronic Computer

Tommy Flowers' experience with Heath Robinson and his knowledge of electronic valves made him realize that a much better machine could be built using electronics. Instead of reading the key stream from a paper tape, an electronically generated key stream would allow for much faster and more flexible processing. Flowers suggested building a machine that was entirely electronic, with one to two thousand valves. Many people at the Telecommunications Research Establishment and Bletchley Park thought this was impossible, believing it would be "too unreliable." However, he had the support of W Gordon Radley, and he built Colossus, the world's first electronic, digital, and somewhat programmable computer, in just ten months. He was helped by his colleagues at the Post Office Research Station Dollis Hill.
The first Colossus (Mark 1), with 1500 valves, started working at Dollis Hill in December 1943. It was used at Bletchley Park by February 1944. It processed messages at 5000 characters per second. It quickly became clear that this was a huge step forward in breaking Tunny. More Colossus machines were ordered, and orders for more Robinsons were canceled. An improved Mark 2 Colossus, with 2400 valves, first worked at Bletchley Park on June 1, 1944, just in time for the D-day Normandy landings.
The main parts of this machine were:
- A tape transport and reading system (the "bedstead") that ran the message tape in a loop at 5000 characters per second.
- A unit that created the key stream electronically.
- Five parallel processing units that could be programmed to do many different logic operations (in the Mark II Colossus).
- Five counting units that each counted the number of `•`s or `x`s. If the count went over a set total, it would print it out.
The five parallel processing units allowed Tutte's "1+2 break in" and other functions to run at an effective speed of 25,000 characters per second. This was done using a circuit invented by Flowers, now called a shift register. Donald Michie figured out a way to use Colossus to help with wheel breaking as well as wheel setting in early 1944. This was then built into special hardware on later Colossus machines.
A total of ten Colossus computers were in use, and an eleventh was being built when the war in Europe ended (VE-Day). Of the ten, seven were used for "wheel setting" and three for "wheel breaking."
Special Machines
Besides the regular teleprinters, other machines were built to help prepare and check tapes in the Newmanry and Testery. Here's a list of machines used in May 1945:
| Name | Function | Testery | Newmanry |
|---|---|---|---|
| Super Robinson | Used for "crib runs" where two tapes were compared in all positions. Had some electronic valves. | 2 | |
| Colossus Mk.2 | Counted a condition involving a message tape and an electronically generated key stream that copied the Tunny wheels. Had about 2,400 valves. | 10 | |
| Dragons | Used for setting short cribs by "crib-dragging." | 2 | |
| Aquarius | A machine being developed at the end of the war. It stored message tape content in electronic memory. | 1 | |
| Proteus | A machine for using depths that was being built but not finished. | ||
| Decoding Machines | Translated typed ciphertext into printed plaintext. Some later ones were faster with valves. | 13 | |
| Tunnies | See British Tunny above. | 3 | |
| Miles | A set of increasingly complex machines (A, B, C, D) that read two or more tapes and combined them in various ways to make an output tape. | 3 | |
| Garbo | Similar to Junior, but with a Differencing feature – used for "rectangling." | 3 | |
| Juniors | For printing tapes through a plug panel to change characters as needed, used to print "de-chis." | 4 | |
| Insert machines | Similar to Angel, but with a device for making corrections by hand. | 2 | |
| Angels | Copied tapes. | 4 | |
| Hand perforators | Made tape from a keyboard. | 2 | |
| Hand counters | Measured text length. | 6 | |
| Stickers (hot) | Used glue and heat to stick tapes together to make a loop. | 3 | |
| Stickers (cold) | Stuck tapes without heating. | 6 |
Steps in Wheel Setting
To figure out the starting position of the chi (χ) wheels, their cam settings first had to be found by "wheel breaking." At first, this was done when two messages were sent with the same settings (in "depth").
The number of starting positions for the first two wheels, χ1 and χ2, was 41×31 = 1271. The first step was to try all these starting positions against the message tape. This was Tutte's "1+2 break in". It involved calculating (∆Z1 ⊕ ∆Z2 ⊕ ∆χ1 ⊕ ∆χ2) – which gives a possible (∆D1 ⊕ ∆D2) – and counting how many times this resulted in a `•`. Incorrect starting positions would, on average, give a `•` count of 50% of the message length. A correct starting point would average 54%, but there was a range of values around these averages.
Both Heath Robinson and Colossus were designed to automate this process. Statistical theory helped measure how far any count was from the expected 50% for an incorrect starting point. This measure was called "sigma." Starting points that gave a count less than 2.5 times sigma were not printed. Ideally, a run to set χ1 and χ2 would produce one outstanding sigma value, clearly identifying the correct starting positions for the first two chi wheels. Here's an example of output from a Mark 2 Colossus:
| χ1 | χ2 | Counter | Count | Operator's notes on the output |
|---|---|---|---|---|
| 06 | 11 | a | 4921 | |
| 06 | 13 | a | 4948 | |
| 02 | 16 | e | 4977 | |
| 05 | 18 | b | 4926 | |
| 02 | 20 | e | 4954 | |
| 05 | 22 | b | 4914 | |
| 03 | 25 | d | 4925 | |
| 02 | 26 | e | 5015 | ← 4.6 σ |
| 19 | 26 | c | 4928 | |
| 25 | 19 | b | 4930 | |
| 25 | 21 | b | 5038 | ← 5.1 σ |
| 29 | 18 | c | 4946 | |
| 36 | 13 | a | 4955 | |
| 35 | 18 | b | 4926 | |
| 36 | 21 | a | 5384 | ← 12.2 σ ch χ1 χ2 ! ! |
| 36 | 25 | a | 4965 | |
| 36 | 29 | a | 5013 | |
| 38 | 08 | d | 4933 |
For an average message, this would take about eight minutes. But by using the Mark 2 Colossus's ability to do multiple things at once, the number of times the message had to be read could be reduced by five times. After finding possible χ1, χ2 starting positions, the next step was to find the starting positions for the other chi wheels. In the example above, one setting (χ1 = 36 and χ2 = 21) stands out with a very high sigma value. This wasn't always the case. Max Newman created decision trees, and Jack Good and Donald Michie designed others. These were used by the Wrens to make choices without needing to ask the codebreakers, if certain rules were met.
In the example above, the next step was to run the first two chi wheels at their found starting positions and explore the remaining three chi wheels in three separate parallel searches. This was called a "short run" and took about two minutes.
| χ1 | χ2 | χ3 | χ4 | χ5 | Counter | Count | Operator's notes on the output |
|---|---|---|---|---|---|---|---|
| 36 | 21 | 01 | a | 2938 | ← 6.8 ρ ! χ3 ! | ||
| 36 | 21 | 01 | b | 2763 | |||
| 36 | 21 | 01 | c | 2803 | |||
| 36 | 21 | 02 | b | 2733 | |||
| 36 | 21 | 04 | c | 3003 | ← 8.6 ρ ! χ5 ! | ||
| 36 | 21 | 06 | a | 2740 | |||
| 36 | 21 | 07 | c | 2750 | |||
| 36 | 21 | 09 | b | 2811 | |||
| 36 | 21 | 11 | a | 2751 | |||
| 36 | 21 | 12 | c | 2759 | |||
| 36 | 21 | 14 | c | 2733 | |||
| 36 | 21 | 16 | a | 2743 | |||
| 36 | 21 | 19 | b | 3093 | ← 11.1 ρ ! χ4 ! | ||
| 36 | 21 | 20 | a | 2785 | |||
| 36 | 21 | 22 | b | 2823 | |||
| 36 | 21 | 24 | a | 2740 | |||
| 36 | 21 | 25 | b | 2796 | |||
| 36 | 21 | 01 | b | 2763 | |||
| 36 | 21 | 07 | c | 2750 |
So the likely starting positions for the chi wheels are: χ1 = 36, χ2 = 21, χ3 = 01, χ4 = 19, χ5 = 04. These had to be checked before the "de-chi" (D) message was sent to the Testery. This check involved Colossus counting how often each of the 32 characters appeared in ΔD. Small called this frequency count the "acid test." Almost every codebreaker and Wren in the Newmanry and Testery knew the following table by heart:
| Char. | Count | Char. | Count | Char. | Count | Char. | Count | |||
|---|---|---|---|---|---|---|---|---|---|---|
| / | 1.28 | R | 0.92 | A | 0.96 | D | 0.89 | |||
| 9 | 1.10 | C | 0.90 | U | 1.24 | F | 1.00 | |||
| H | 1.02 | V | 0.94 | Q | 1.01 | X | 0.87 | |||
| T | 0.99 | G | 1.00 | W | 0.89 | B | 0.82 | |||
| O | 1.04 | L | 0.92 | 5 | 1.43 | Z | 0.89 | |||
| M | 1.00 | P | 0.96 | 8 | 1.12 | Y | 0.97 | |||
| N | 1.00 | I | 0.96 | K | 0.89 | S | 1.04 | |||
| 3 | 1.13 | 4 | 0.90 | J | 1.03 | E | 0.89 |
If the found starting points of the chi wheels passed this test, the "de-chi-ed" message was sent to the Testery. There, manual methods were used to find the psi and motor settings. As Small noted, the Newmanry's work involved a lot of statistical science, while the Testery's work required great language knowledge and was seen as an art. Codebreaker Jerry Roberts pointed out that the Testery's work was a heavier burden on staff than the automated processes in the Newmanry.
Images for kids
-
A Lorenz SZ42 cipher machine with its covers removed at The National Museum of Computing on Bletchley Park.
-
A typical distribution of letters in English language text. Poor scrambling might not hide this pattern. This weakness was used to break the Lorenz cipher.
-
A rebuilt British Tunny at the National Museum of Computing, Bletchley Park. It copied the functions of the Lorenz SZ40/42, printing clear text from scrambled input.
-
In 1994, a team led by Tony Sale (right) began rebuilding a Mark 2 Colossus at Bletchley Park. Here, in 2006, Sale and Phil Hayes supervise the solving of a scrambled message with the completed machine.