Galois theory facts for kids

Galois theory (pronounced gal-wah) is a special part of mathematics. It connects two important math ideas: fields and groups.

Think of fields as sets of numbers. You can add, subtract, multiply, and divide these numbers. Groups are similar, but they usually have only one main operation, like addition. Fields can be tricky to study because they have so many possible number combinations. Groups are often simpler and easier to understand. Galois theory helps us connect these hard-to-study fields with easier-to-study groups. This connection makes it possible to solve some very old math puzzles.

Historical Math Puzzles

For a long time, mathematicians faced some big questions they couldn't answer.

Euclid's Ancient Problems

Around 300 BCE, a Greek mathematician named Euclid wrote a famous book called Elements. It was all about geometry. Euclid showed how to do many things with just a straightedge and compass. For example, he could cut any angle exactly in half. He could also draw shapes like triangles, squares, and pentagons.

But Euclid and other mathematicians couldn't draw every shape. For instance, they couldn't make a regular 9-sided shape (a 9-gon) using only a straightedge and compass. They also wondered:

• Could they cut any angle into three equal parts? (This is called trisecting an angle.)
• Could they make a square with the exact same area as a circle? (This is called squaring the circle.)
• Could they make a cube that was exactly twice the volume of another cube? (This is called doubling the cube.)

These questions remained unsolved for over 2,000 years!

The Mystery of Formulas for Equations

You might have learned about polynomial equations in school. These are equations where you add and subtract different powers of a variable, like . The degree of a polynomial is the highest power of the variable in the equation.

A common polynomial is a quadratic equation. Its highest power is two, like . You probably know the quadratic formula to solve these: 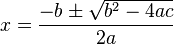This formula gives you the answers (called roots) just by plugging in the numbers .

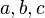Mathematicians hoped to find similar simple formulas for any polynomial equation. They wanted formulas that used only addition, subtraction, multiplication, division, powers, and roots. They found formulas for polynomials with degree 3 and degree 4.

However, no one could ever find a formula for polynomials with degree 5 or higher. Why not? What was stopping them? This was a huge puzzle.

Fields and Groups: The Key

The answers to these old problems came from studying fields and groups. It turns out that every equation has a special field and a special group connected to it.

What are Fields?

The field linked to an equation has a complex structure. But you can learn a lot about it by seeing how you can rearrange its elements without changing its basic structure.

What are Groups and S_n?

All the ways you can rearrange or "shuffle" a field's elements can be turned into a group. There are special groups called the Symmetric Group on n elements, written as S_n. These groups show all the ways to shuffle n different things.

Symmetric groups are easy to understand when you shuffle 1, 2, 3, or 4 things. But if you shuffle 5 or more things, the structure of the symmetric group becomes very complicated and "chaotic."

Galois's Big Discovery

Évariste Galois, who at just 18 years old, created the theory named after him.

Before the early 1800s, mathematicians found some answers for specific math problems. But they couldn't explain why these answers worked or why other problems were impossible.

Then came a young French mathematician named Évariste Galois (born October 25, 1811 – died May 31, 1832). He was the first to find a solution. He explained why equations of degree 2, 3, and 4 had nice solution formulas, but equations of degree 5 and higher could not have a general formula.

Galois proved that the problem of solving equations could be linked to understanding their groups. He showed that the equation's field and its group had a deep connection.

Galois's Key Idea

Galois realized that the groups connected to polynomials were actually just symmetric groups in disguise. If a polynomial had a degree of n, its group was the symmetric group on n elements (S_n). Galois saw that the group of an equation shuffled the answers (roots) of the polynomial. He found that he could study the structure of these shuffles instead of the complicated equations themselves.

Solving Euclid's Old Problems

Euclid wanted to cut any angle into three equal parts. Galois used his theory to show that if you could do this with a ruler and compass, it would involve an equation of degree 3. By looking at the equation's group and field, he proved that only angles related to powers of two could be made. This meant that trisecting an arbitrary angle was impossible.

Galois's theory also showed that it was impossible to square a circle or double a cube using only a straightedge and compass.

Why Some Polynomials Had Formulas

Galois also used his theory to explain why polynomials of degree 5 and higher didn't have general formulas. He showed that if an equation could be solved with a simple formula, then its group would have a "nice" and predictable structure.

However, the symmetric group S_n becomes "chaotic" when n is 5 or larger. Since the groups of degree 5 and higher polynomials were chaotic, Galois proved that no general formula could exist for them.

See also

In Spanish: Teoría de Galois para niños