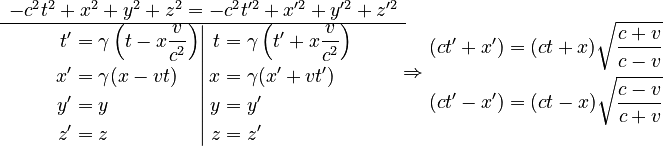History of Lorentz transformations facts for kids

Kids Encyclopedia Facts

The Lorentz transformations are a set of special mathematical rules. They help us understand how measurements of space and time change when things move very, very fast. This is especially true when objects move close to the speed of light.

These transformations are super important in special relativity. This is a famous theory by Albert Einstein. They show us that the speed of light is always the same for everyone. It doesn't matter how fast you are moving. The transformations help us compare where and when an event happens. This is done from the viewpoint of two different observers who are moving at a steady speed relative to each other.

Early Math Ideas
Electrodynamics and Special Relativity
See also

Early Math Ideas

Long before they were used in physics, similar mathematical ideas were explored in the 1800s. These ideas were part of studies on shapes and spaces. They looked at things like hyperbolic geometry. This is a type of geometry where parallel lines can meet. These early math concepts helped set the stage for the Lorentz transformations.

Electrodynamics and Special Relativity

The Lorentz transformations became well-known in the early 1900s. Scientists found they were key to understanding Maxwell's equations. These equations describe how electricity and magnetism work. Later, these transformations became a basic part of all physics. They form the foundation of special relativity. They show how Minkowski spacetime works. This is a way of thinking about space and time together.

The transformations help us connect measurements of time and position. Imagine one person measuring an event as x,y,z for position and t for time. Another person moving at a constant speed v would measure the same event as x′,y′,z′ and t′.

Here are the main equations for Lorentz transformations in 3+1 dimensions (3 for space, 1 for time):

\begin{matrix}-c^{2}t^{2}+x^{2}+y^{2}+z^{2}=-c^{2}t^{\prime2}+x^{\prime2}+y^{\prime2}+z^{\prime2}\\ \hline \left.\begin{align}t' & =\gamma\left(t-x\frac{v}{c^{2}}\right)\\ x' & =\gamma(x-vt)\\ y' & =y\\ z' & =z \end{align} \right|\begin{align}t & =\gamma\left(t'+x\frac{v}{c^{2}}\right)\\ x & =\gamma(x'+vt')\\ y & =y'\\ z & =z' \end{align} \end{matrix}\Rightarrow\begin{align}(ct'+x') & =(ct+x)\sqrt{\frac{c+v}{c-v}}\\ (ct'-x') & =(ct-x)\sqrt{\frac{c-v}{c+v}} \end{align}

Many scientists contributed to developing these ideas. This includes Woldemar Voigt, Oliver Heaviside, Joseph John Thomson, George Frederick Charles Searle, Hendrik Lorentz, Joseph Larmor, Henri Poincaré, and Albert Einstein.

Voigt's Early Work (1887)

Woldemar Voigt created a transformation in 1887. It was related to how sound or light waves change frequency (the Doppler effect). His equations were similar to the modern Lorentz transformations. However, they also included a "rescaling" of space and time. This meant that the size of things could change.

Voigt's theory said the speed of light was constant. But his transformations mixed a relativistic change with a size change. Later, scientists like Poincaré and Einstein showed that for the rules to work for everything in physics, the size change factor had to be exactly 1. This made the Lorentz transformation the correct choice.

Early Electromagnetism Studies

In the late 1800s, scientists studied how electric charges behave when they move.

In 1888, Oliver Heaviside looked at the electric field around moving charges. He found that the field would change shape.
Joseph John Thomson (1889) found a way to simplify calculations for moving charges. He used a mathematical transformation.
George Frederick Charles Searle (1896) noticed that Heaviside's work meant electric fields would get squashed. He called this the "Heaviside-Ellipsoid."

Lorentz's Contributions (1892, 1895)

Hendrik Lorentz worked to explain how light behaves. He wanted to understand why the Fizeau experiment and aberration of light happened. In 1892, he developed a model where light travels through a motionless "aether." He introduced new quantities to transform measurements. These were similar to the Lorentz transformation.

Lorentz also suggested that objects moving through the aether would shrink. This idea, called length contraction, helped explain the Michelson–Morley experiment. He thought of time in two ways: "true" time for observers in the aether and "local time" for moving observers. He used "local time" as a helpful mathematical tool.

In 1895, Lorentz refined his ideas. He showed that a moving observer would see the same things as a resting observer. This was true if they used his special transformations. He used "local time" to explain the Doppler effect and other light phenomena.

Larmor's Work (1897, 1900)

Joseph Larmor expanded on Lorentz's work in 1897. He derived transformations that were very close to the full Lorentz transformations. He was the first to realize that these transformations meant time itself would slow down for moving objects. This is called time dilation. He showed that Maxwell's equations remained the same under these transformations.

In his 1900 book, Larmor used a modified "local time." He showed that Maxwell's equations were invariant under these transformations. This means the equations look the same no matter how fast you are moving.

Lorentz's Later Work (1899, 1904)

Lorentz continued to improve his theory. In 1899, he introduced a factor that he couldn't fully explain. But when this factor was set to 1, his transformations became the complete Lorentz transformations. He also noticed a time dilation effect.

In 1904, Lorentz showed that a certain factor in his equations must be 1. This meant that length contraction only happens in the direction of motion. He also realized that these transformations should apply to all forces in nature, not just electrical ones. However, he still struggled to make all equations fully consistent with the principle of relativity.

Poincaré's Contributions (1900, 1905)

Henri Poincaré was a brilliant mathematician.

Local Time Explained

In 1900, Poincaré explained Lorentz's "wonderful invention" of local time. He said it came from how clocks are synchronized. If you send light signals between clocks, and assume light travels at the same speed in all directions, you get "local time." This led to the idea that events that seem simultaneous to one person might not be simultaneous to another. This is called relativity of simultaneity.

Naming the Lorentz Transformation

On June 5, 1905, Poincaré wrote down the transformation equations in their modern form. He was the first to call them the "Lorentz transformation." He also showed that these transformations form a "group." This means that if you apply one transformation and then another, the result is also a valid transformation. He also showed that the combination x²+y²+z²-t² stays the same. He even saw the Lorentz transformation as a rotation in a four-dimensional space.

Einstein and Special Relativity (1905)

On June 30, 1905, Albert Einstein published his theory of special relativity. He provided a new way to understand the Lorentz transformations. His derivation was based on two simple ideas:

The principle of relativity: The laws of physics are the same for all observers moving at a constant speed.
The principle of the constancy of the speed of light: The speed of light in empty space is always the same, no matter the motion of the light source or the observer.

Einstein showed that "local time" was not just a mathematical trick. It was the actual time measured by observers in different moving frames. Unlike Lorentz and Poincaré, Einstein didn't need a "mechanical aether." He showed that the transformations applied to how space and time themselves behave.

Einstein's equations for the transformation were similar to Poincaré's. He also defined how velocities add up in special relativity. This is different from how they add up in everyday life. He also explained the aberration of light. This is why stars appear to shift slightly in position as Earth moves.

Minkowski and Spacetime (1907–1908)

Hermann Minkowski took the ideas of Lorentz, Einstein, and Poincaré further. In 1907 and 1908, he combined them into a new concept: Minkowski spacetime. He showed that space and time are not separate. Instead, they are woven together into a single four-dimensional fabric.

Minkowski used imaginary numbers to represent time. He showed that the Lorentz transformation is like a rotation in this four-dimensional spacetime. He also introduced the Minkowski diagram. This is a visual tool that helps us understand how events look in spacetime for different observers. It's still used in textbooks today.

Original spacetime diagram by Minkowski in 1908.

Other Mathematical Approaches

Many other scientists explored different mathematical ways to describe the Lorentz transformations:

Arnold Sommerfeld (1909) used imaginary trigonometric functions.
Philipp Frank (1909) and Vladimir Varićak (1910) used hyperbolic functions. These are special mathematical functions related to hyperbolas.
Harry Bateman and Ebenezer Cunningham (1909–1910) looked at spherical wave transformations.
Gustav Herglotz (1909–10) used Möbius transformations.
Henry Crozier Keating Plummer (1910) and Paul Gruner (1921) used trigonometric functions for Lorentz boosts.
Vladimir Ignatowski (1910) showed that the transformations could be derived using only the principle of relativity. He didn't need to assume the speed of light was constant.
Fritz Noether (1910), Felix Klein (1910), Arthur W. Conway (1911), and Ludwik Silberstein (1911) used quaternions. These are a type of complex number system.
Émile Borel (1913–14) used Cayley–Hermite parameters.

These different mathematical approaches all showed the same underlying rules. They helped scientists understand the Lorentz transformations from many angles.