Measure (mathematics) facts for kids
In mathematics, a measure is a way to give a "size" to parts of a set. Think of it like measuring length, area, or volume in geometry. It's also used for things like mass or the probability of an event happening.
These different ideas of "size" actually have a lot in common. Mathematicians created the idea of a "measure" to study them all together. Measures are super important in probability theory (which deals with chance) and integration theory (which is about adding up tiny pieces).
The basic idea of measuring things goes back to ancient Greece. For example, Archimedes tried to figure out the area of a circle. But the modern mathematical theory of measures only really started in the late 1800s and early 1900s. Many smart mathematicians like Henri Lebesgue helped build this field.
Contents
What is a Measure?
Imagine you have a big set of things, let's call it 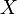 . A measure is like a special rule that tells you the "size" of certain parts (or subsets) of
. A measure is like a special rule that tells you the "size" of certain parts (or subsets) of 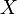 . These parts must be "measurable sets," which means they are part of a special collection called a
. These parts must be "measurable sets," which means they are part of a special collection called a 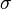 -algebra.
-algebra.
For something to be called a "measure," it must follow these rules:
- No Negative Sizes: The "size" (measure) of any part must be zero or a positive number. You can't have a negative length or area!
- Empty Set is Zero: The measure of an empty set (a set with nothing in it) is always 0.
- Adding Up Pieces: If you have a collection of parts that don't overlap (they are disjoint sets) and you combine them, the measure of the combined part is the sum of the measures of each individual part. This is called countable additivity. For example, if you have two separate pieces of land, the total area is the sum of their individual areas.
When you have a set 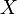 and a collection of its measurable parts, it's called a measurable space. If you add a measure to it, it becomes a measure space.
and a collection of its measurable parts, it's called a measurable space. If you add a measure to it, it becomes a measure space.
A special type of measure is a probability measure. This is a measure where the "size" of the entire set 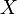 is exactly 1. This is useful for probabilities, where the chance of something definitely happening is 1 (or 100%).
is exactly 1. This is useful for probabilities, where the chance of something definitely happening is 1 (or 100%).
Examples of Measures
There are many different types of measures used in mathematics and science:
- Counting Measure: This is the simplest measure! It just counts how many items are in a set. For example, the counting measure of the set {apple, banana, orange} is 3.
- Lebesgue Measure: This is the most common measure in everyday life. It's used to find the length of lines, the area of shapes, and the volume of objects in space. For example, the Lebesgue measure of a line segment from 0 to 1 is 1.
- Probability Measure: As mentioned, this measure tells you the chance of an event happening. The total probability of all possible outcomes is always 1. For example, the probability measure of flipping a coin and getting heads is 0.5.
- Dirac Measure: This measure is special because it only "sees" if a specific point is in a set. If the set contains that point, its measure is 1; otherwise, it's 0. Imagine a tiny sensor that only detects if a specific grain of sand is present.
- Haar Measure: This is a more advanced measure, but it's like a generalized Lebesgue measure for certain mathematical structures called "topological groups." It helps measure "size" in a way that stays the same even if you move or rotate things.
- Hausdorff Measure: This measure is used for more complex shapes, like fractals, which can have "dimensions" that aren't whole numbers (like 1.5 or 2.3).
In physics, measures are used to describe things like the distribution of mass in space. For example, how much mass is in a certain region.
Basic Rules of Measures
Let's look at some basic rules that all measures follow:
Monotonicity
If you have two measurable sets, 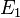 and
and 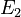 , and
, and 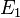 is completely inside
is completely inside 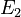 (meaning
(meaning 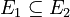 ), then the measure of
), then the measure of 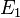 will always be less than or equal to the measure of
will always be less than or equal to the measure of 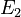 . This makes sense: a smaller piece can't have a larger size than a bigger piece that contains it!
. This makes sense: a smaller piece can't have a larger size than a bigger piece that contains it!
Measure of Combined Sets
Countable Subadditivity
If you have a collection of measurable sets 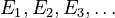 (they don't have to be separate), the measure of their combined total (their union) will be less than or equal to the sum of their individual measures. It's like saying if you overlap some pieces of paper, the total area they cover is less than or equal to the sum of their individual areas.
(they don't have to be separate), the measure of their combined total (their union) will be less than or equal to the sum of their individual measures. It's like saying if you overlap some pieces of paper, the total area they cover is less than or equal to the sum of their individual areas.
Continuity from Below
Imagine you have a sequence of measurable sets that are growing bigger and bigger, with each set containing the previous one (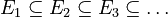 ). As these sets grow, their measures get closer and closer to the measure of their final, combined set (their union).
). As these sets grow, their measures get closer and closer to the measure of their final, combined set (their union).
Continuity from Above
Now imagine you have a sequence of measurable sets that are shrinking, with each set being contained within the previous one (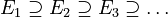 ). If at least one of these sets has a finite (not infinite) measure, then as these sets shrink, their measures get closer and closer to the measure of their final, overlapping part (their intersection).
). If at least one of these sets has a finite (not infinite) measure, then as these sets shrink, their measures get closer and closer to the measure of their final, overlapping part (their intersection).
Other Important Ideas
Completeness
A measurable set 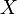 is called a null set if its measure is 0. Think of a single point on a line; its length (Lebesgue measure) is 0, so it's a null set. A part of a null set is called a negligible set.
is called a null set if its measure is 0. Think of a single point on a line; its length (Lebesgue measure) is 0, so it's a null set. A part of a null set is called a negligible set.
A measure is called complete if every negligible set is also measurable. This means if a set is "small enough" to be part of something with zero measure, then you can also measure it.
Sigma-finite Measures
A measure space is called finite if the measure of the entire space 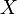 is a finite number (not infinity).
is a finite number (not infinity).
A measure is called σ-finite (pronounced "sigma-finite") if you can break down the entire set 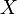 into a countable number of measurable parts, where each part has a finite measure.
into a countable number of measurable parts, where each part has a finite measure.
For example, the set of all real numbers with the standard Lebesgue measure (length) is σ-finite. You can cover the entire real line with countable intervals like [0,1], [1,2], [2,3], and so on, each having a finite measure (length 1).
Non-measurable Sets
It might seem strange, but not every subset of space can be "measured" in a way that follows all the rules of a measure. If we assume a certain mathematical rule called the axiom of choice is true, then it's possible to show that some sets simply don't have a well-defined Lebesgue measure. These are called non-measurable sets. They are very complex and hard to imagine!
Generalizations
Sometimes, mathematicians use "measures" that can take on different kinds of values:
- Signed Measure: This is like a measure, but its values can be negative. Think of electrical charge, which can be positive or negative.
- Complex Measure: This is a measure whose values can be complex numbers (numbers that include an imaginary part).
- Finitely Additive Measure: This is an older idea, where the "adding up pieces" rule only applies to a finite number of parts, not an infinite (countable) number.
See also
- Almost everywhere
- Fubini's theorem
- Lebesgue integration
- Lebesgue measure
- Measurable function
- Probability measure
- Product measure
- Signed measure
- Volume form



 is a
is a  the measure of
the measure of  Furthermore, the measure of the
Furthermore, the measure of the 
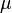 : The measure of a countable disjoint union is the same as the sum of all measures of each subset.
: The measure of a countable disjoint union is the same as the sum of all measures of each subset.