Natural number facts for kids
|
Natural numbers, also called counting numbers, are the numbers we use to count things. Think of them as the numbers you learn first, like 1, 2, 3, and so on.
Sometimes, the number zero (0) is also considered a natural number. Other times, one is seen as the smallest natural number. Natural numbers are always whole numbers and are never less than zero.
There is no largest natural number. You can always find the next one by adding 1. This means they go on "for ever." You can reach any natural number by adding 1 enough times to the smallest natural number.
Contents
What are Non-Natural Numbers?
Not all numbers are natural numbers. Here are some types of numbers that are not natural numbers:
- Negative numbers: These are numbers less than 0, like −2 or −1.
- Fractions: These are parts of a whole, like ½ or 3¼.
- Decimals: These are numbers with a decimal point, like 7.675.
- Irrational numbers: These are numbers that cannot be written as a simple fraction. Examples include
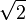 or
or 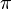 (pi).
(pi). - Imaginary numbers: These are special numbers that come from the square root of a negative number, like
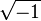 (called i).
(called i). - Infinity: This is a concept meaning "endless" or "without limit," not a specific number. It's shown as
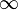 .
.
Basic Math with Natural Numbers
Natural numbers follow some simple rules when you do math with them.
Adding Natural Numbers
When you add two natural numbers, the answer is always another natural number.
- If you add l and m to get n, it looks like:
 .
. - The order doesn't matter:
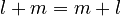 .
. - Adding zero doesn't change the number:
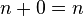 .
. - When adding three numbers, you can group them differently:
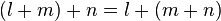 .
.
Multiplying Natural Numbers
When you multiply two natural numbers, the answer is always another natural number.
- If you multiply l and m to get n, it looks like:
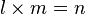 .
. - The order doesn't matter:
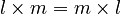 .
. - Multiplying by zero always gives zero:
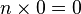 .
. - Multiplying by one doesn't change the number:
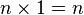 .
. - When multiplying three numbers, you can group them differently:
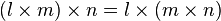 .
. - You can also combine addition and multiplication:
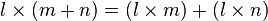 .
.
Ordering Natural Numbers
Natural numbers can be put in order. If two numbers are not the same, one is always bigger or smaller than the other.
- We use symbols like: m = n (equal), m > n (greater than), or m < n (less than).
- If l is greater than m (l > m), then:
- Adding the same number to both keeps the order:
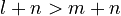 .
. - Multiplying both by a natural number (not zero) keeps the order:
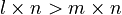 .
.
- Adding the same number to both keeps the order:
- Zero is the smallest natural number:
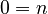 or
or 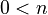 .
. - There is no largest natural number because you can always find one bigger:
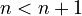 .
.
Subtracting Natural Numbers
Subtraction can sometimes result in a natural number.
- If n is smaller than m, then m minus n is a natural number. For example, if n < m, then
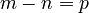 .
. - If
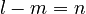 , then
, then 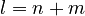 .
. - If n is greater than m, then m minus n is not a natural number (it would be a negative number).
Dividing Natural Numbers
Division can also result in a natural number.
- If
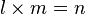 , then
, then 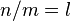 . This means if you can multiply two natural numbers to get a third, then dividing the third by one of them gives the other.
. This means if you can multiply two natural numbers to get a third, then dividing the third by one of them gives the other.
Mathematical Induction
This is a powerful way to prove things about all natural numbers. If two things are true about a property P of natural numbers, then P is true for every natural number:
- P is true for 0.
- If P is true for any number n, then P is also true for n+1.
Special Natural Numbers
Some natural numbers have special names based on their properties.
Even Numbers
- An even number is any number that can be divided by 2 without a remainder.
- If
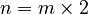 , then n is an even number.
, then n is an even number. - The even numbers are 0, 2, 4, 6, and so on. Zero is usually considered the smallest even number.
Odd Numbers
- An odd number is a number that is not even. When you divide an odd number by 2, there's always a remainder of 1.
- If
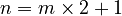 , then n is an odd number.
, then n is an odd number. - A number is either even or odd, but not both.
- The odd numbers are 1, 3, 5, 7, and so on.
Composite Numbers
- A composite number is a natural number that can be made by multiplying two smaller natural numbers (other than 0 or 1).
- If
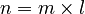 , and m and l are not 0 or 1, then n is a composite number.
, and m and l are not 0 or 1, then n is a composite number. - The composite numbers are 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 21, and so on.
Prime Numbers
- A prime number is a natural number greater than 1 that has only two factors: 1 and itself. It cannot be made by multiplying two smaller natural numbers (other than 1).
- If a number is not 0, 1, and not a composite number, then it is a prime number.
- The prime numbers are 2, 3, 5, 7, 11, 13, 17, and so on.
- Two is the smallest prime number and the only even prime number.
- There is no biggest prime number; they go on forever!
Square Numbers
- A square number is a number you get by multiplying a natural number by itself.
- If
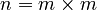 , then n is a square number. We say n is the square of m.
, then n is a square number. We say n is the square of m. - The square numbers are 0, 1, 4, 9, 16, 25, 36, 49, and so on.
How to Write Natural Numbers in Math
In mathematics, we often use symbols to represent the set of all natural numbers. 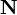 or
or 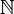 are common ways to write this set.
are common ways to write this set.
Since some people include 0 as a natural number and some don't, different symbols are used to be clear:
| Symbol | Meaning |
|---|---|
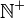 |
Positive numbers, without zero (1, 2, 3, ...) |
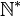 |
Positive numbers without zero (1, 2, 3, ...) |
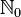 |
Positive numbers, with zero (0, 1, 2, 3, ...) |
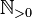 |
Positive numbers without zero (1, 2, 3, ...) |
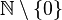 |
Positive numbers without zero (1, 2, 3, ...) |
Related Pages
See also
 In Spanish: Número natural para niños
In Spanish: Número natural para niños


