Tower of Hanoi facts for kids

A model set of the Tower of Hanoi (with 8 disks)

An animated solution of the Tower of Hanoi puzzle for T(4, 3)

Tower of Hanoi interactive display at the Universum museum in Mexico City

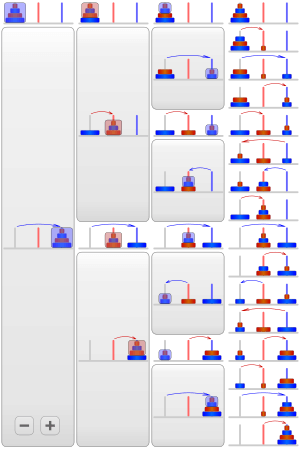
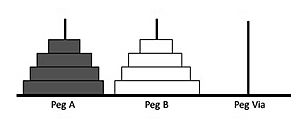
The Tower of Hanoi is a fun mathematical game or puzzle. It has three tall rods and several disks of different sizes. These disks can slide onto any rod. The puzzle starts with all the disks neatly stacked on one rod. The largest disk is at the bottom, and they get smaller as you go up, forming a cone shape.

The main goal of the puzzle is to move the entire stack of disks to the last rod. You must follow these simple rules:

• Only one disk can be moved at a time.
• Each move involves taking the top disk from one stack and placing it on top of another stack or an empty rod.
• You can never place a larger disk on top of a smaller disk.

If you have 3 disks, you can solve the puzzle in just 7 moves. The smallest number of moves needed to solve the Tower of Hanoi puzzle is found using the formula 2ⁿ − 1. Here, n is the number of disks you are using.

History of the Puzzle

The Tower of Hanoi puzzle was created by a French mathematician named Édouard Lucas in 1883. Soon after, many exciting stories and myths about the puzzle's ancient origins appeared.

One famous story tells of an Indian temple in Kashi Vishwanath. This temple supposedly has a large room with three old posts and 64 golden disks. Brahmin priests, following an ancient prophecy, have been moving these disks according to the puzzle's rules ever since. Because of this legend, the puzzle is also known as the Tower of Brahma. The legend says that when the very last disk is moved, the world will end!

If this legend were true, and if the priests could move one disk every second, it would take them an incredibly long time to finish. With 64 disks, it would take 2⁶⁴ − 1 seconds. That's about 585 billion years! This is about 42 times older than our universe is right now.

There are many versions of this legend. Some say the temple is a monastery and the priests are monks. The location might change too, sometimes it's said to be in Hanoi, Vietnam. Some stories even add that the tower was made at the beginning of the world, or that the monks can only make one move per day.

How to Solve the Puzzle

You can play the Tower of Hanoi with any number of disks. Many toy versions come with about 7 to 9 disks. The fewest moves needed to solve the puzzle is always 2ⁿ − 1, where n is the number of disks.

Step-by-Step Solution

Animation of a step-by-step way to solve the 6-disk problem

A simple way to solve the puzzle is to always switch between moving the smallest disk and moving a non-smallest disk.

When you move the smallest disk, always move it in the same direction around the pegs. If you started with an even number of disks, move it to the right. If you started with an odd number of disks, move it to the left. If there's no peg in that direction, move it to the very end, but then keep moving in your chosen direction. For example, with three disks, you'd move the smallest disk to the opposite end first, then continue moving it to the left.

When it's time to move a non-smallest disk, there will only be one correct move you can make without breaking the rules. Following these steps will help you solve the puzzle in the fewest possible moves.

Simple Steps for Solving

Here's an even simpler way to think about the step-by-step solution:

If you have an even number of disks:

• Move a disk between peg A and peg B.
• Move a disk between peg A and peg C.
• Move a disk between peg B and peg C.
• Keep repeating these three types of moves until you're done.

If you have an odd number of disks:

• Move a disk between peg A and peg C.
• Move a disk between peg A and peg B.
• Move a disk between peg B and peg C.
• Keep repeating these three types of moves until you're done.

In both cases, you will make exactly 2ⁿ − 1 moves.

Recursive Solution (Thinking in Parts)

How a recursive solution works for the Towers of Hanoi puzzle with 4 disks

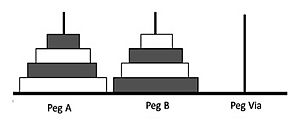
A powerful way to think about solving this puzzle is to break it down into smaller, similar problems. This is called a "recursive" solution. Imagine you want to move n disks from a starting peg (A) to a target peg (C), using a spare peg (B).

Here's how you can do it:

1. First, move the top n − 1 disks from the starting peg (A) to the spare peg (B). You do this by using the same "puzzle-solving method." This leaves the largest disk (disk n) alone on the starting peg.
2. Next, move the largest disk (disk n) from the starting peg (A) to the target peg (C). This is always a valid move because it's the largest disk.
3. Finally, move the n − 1 disks that are now on the spare peg (B) to the target peg (C). Again, you use the same "puzzle-solving method" for these smaller disks. They will stack perfectly on top of disk n.

The simplest case (the "base case") is moving 0 disks, which means you do nothing. This method is often used to teach how to solve problems in computer programming.

Binary and Gray Code Solutions

The way disks move in the Tower of Hanoi puzzle follows patterns related to binary numbers (base-2) and Gray codes.

For example, if you count the moves starting from 1, the disk you need to move on any given turn is related to how many times that move number can be divided by 2. The smallest disk is always involved in every odd-numbered move.

Also, the smallest disk moves in a specific pattern. If you have an odd number of disks, it cycles from the start peg to the target peg, then to the remaining peg, and back to the start. If you have an even number of disks, this cycle is reversed. These patterns help you figure out which disk to move and where, without needing to remember all the previous steps.

Visualizing the Game

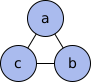
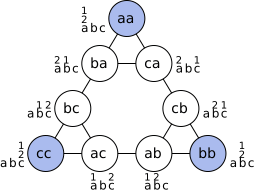
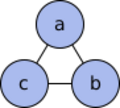
The Tower of Hanoi game can be shown as a type of graph. In this graph, each point (or "node") represents a different way the disks can be arranged on the pegs. The lines (or "edges") between these points show the possible moves you can make.

For just one disk, the graph looks like a simple triangle:

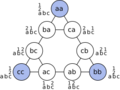
For two disks, the graph looks like three triangles connected at their corners, forming a bigger triangle.

The points at the very corners of the largest triangle show when all the disks are stacked on one peg.

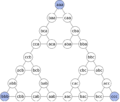
As you add more disks, the graph of the game starts to look like a famous fractal shape called the Sierpiński triangle.

The game graph of level 7 shows the relatedness to the Sierpiński triangle.

This shows that many possible disk arrangements are never reached if you always choose the shortest way to solve the puzzle.

Different Ways to Play

The Tower of Hanoi has many interesting variations:

Adjacent Pegs

Imagine the pegs are in a line (A, B, C). If you can only move disks between pegs that are next to each other (so no direct moves between A and C), then moving a stack of n disks from peg A to peg C takes 3ⁿ − 1 moves. This version uses every possible disk arrangement.

Cyclic Hanoi

In Cyclic Hanoi, the three pegs (A, B, C) are arranged in a circle. You can only move disks in a clockwise direction (A to B, B to C, C to A). This version has its own set of rules for the smallest number of moves. For example, the smallest disk is always the first and last disk to move.

Four Pegs and More

While the original puzzle has three pegs, people have also explored versions with four or more pegs. The best way to solve the Tower of Hanoi with four pegs (called Reve's puzzle) was only fully proven in 2014! For more than three pegs, a method called the Frame–Stewart algorithm is often used, though it's been known since 1941.

Magnetic Hanoi

Initial setup of a 4-disk Bicolor Towers of Hanoi

In Magnetic Tower of Hanoi, each disk has two different sides, like magnets (North and South, or red and blue). You cannot place disks with similar magnetic poles together. Also, each disk must be flipped over every time it is moved.

Bicolor Towers of Hanoi

Final setup of a 4-disk Bicolor Towers of Hanoi

This version was even given to students in a math competition! The basic rules are the same: move one disk at a time, and no larger disk on a smaller one. The difference is that for each disk size, there are two disks: one black and one white. The puzzle starts with two towers of disks, alternating colors. The goal is to make the towers all one color.

Tower of Hanoy (Card Game)

A card game version of the puzzle exists, using nine playing cards. It's called "Tower of Hanoy," with a slightly different spelling. It's not known if this spelling change was on purpose or by accident.

Real-World Uses

The Tower of Hanoi is more than just a game!

• It's often used in psychology studies to understand how people solve problems.
• A similar task, called the Tower of London Test, helps doctors diagnose and treat brain function issues.
• The puzzle has influenced how we design computer programs and human–computer interaction.
• It's also used as a plan for organizing computer data backups using multiple tapes or media.
• Many computer programming students learn about "recursive algorithms" by studying the Tower of Hanoi. You can even find a version of it built into the emacs computer editor!
• Neuropsychologists use it as a test to check for problems with the frontal lobe of the brain.
• In 2010, scientists found that tiny ant species called Linepithema humile could actually solve the 3-disk Tower of Hanoi problem using their natural signals!
• In 2014, scientists even created tiny, layered materials that look like the Tower of Hanoi.

Images for kids

See also

In Spanish: Torres de Hanói para niños